题目内容
若f（a）＝（3m－1）a＋b－2m，当m∈[0,1]时f（a）≤1恒成立，则a＋b的最大值为
A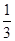． | B． | C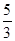． | D． |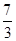
D
解析试题分析：先根据恒成立写出有关a，b的约束条件，再在aob系中画出可行域，设z=a+b，利用z的几何意义求最值，只需求出直线a+b=z过可行域内的点A时z最大值即可.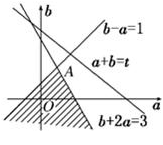
解：设g（m）=f（a）=（3a-2）m+b-a，由于当m∈[0，1]时,g（m）=f（a）=（3a-2）m+b-a≤1恒成立，于是g(0)≤1, g(1)≤1，即b-a≤1, b+2a≤1满足此不等式组的点（a，b）构成图中的阴影部分，其中A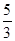（ ，），设a+b=t，显然直线a+b=t过点A时，t取得最大值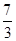故选D．
考点：恒成立问题
点评：本题主要考查了恒成立问题、用平面区域二元一次不等式组，以及简单的转化思想和数形结合的思想，属中档题．目标函数有唯一最优解是我们最常见的问题，这类问题一般要分三步：画出可行域、求出关键点、定出最优解．
练习册系列答案
相关题目
函数
的图象如下图所示，则函数
下列函数中，既是偶函数又在
单调递增的函数是 ( )
A． | B． | C． | D． |
设
、
分别是定义在
上的奇函数和偶函数，当
时，
，且
，则不等式
的解集是（ ）
A． | B． |
C． | D． |
函数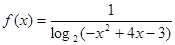
的定义域为（ ）
| A．（1，2）∪（2，3） | B． |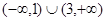
| C．（1，3） | D．[1，3] |
已知函数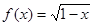
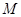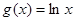定义域为
，
定义域为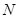
，则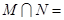
（ ）
A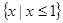． | B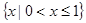． | C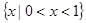． | D． |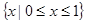
若函数
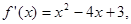的导函数
则函数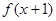
的单调递减区间是（ ）
| A．（2，4） | B．（-3，-1） | C．（1，3） | D．（0，2） |
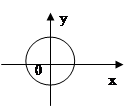
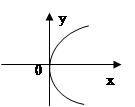
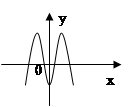
的定义域为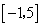
，部分对应值如下表：
的图象如图所示，
是周期函数；
是减函数；
时，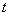
的最大值为4；
时，函数
有4个零点。