题目内容
函数满足f(x)f(x+2)=13,若f(3)=2,则f(2013)= ( )
| A.13 | B.2 | C. | D. |
C
解析试题分析:∵f(x)•f(x+2)=13,∴f(x+2)f(x+4)=13,∴f(x)=f(x+4),∴函数f(x)是周期为4的函数.
∴f(2013)=f(503×4+1)=f(1).
由f(1)•f(3)=13,f(3)=2,∴f(1)=  .
.
∴f(2013)=f(1)= ,故选C。
,故选C。
考点:函数的周期性。
点评:中档题,由已知条件得出函数f(x)是周期函数是解题的关键。此类问题,一般解法就是研究发现函数的性质。

练习册系列答案
相关题目
设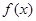 是定义域为
是定义域为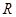 ,最小正周期为
,最小正周期为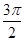 的函数。若
的函数。若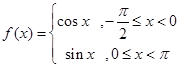 , 则
, 则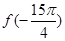 等于( )
等于( )
| A.1 | B.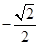 | C.0 | D.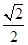 |
函数 与
与 在区间[1,2]上都是减函数,则a的取值范围是
在区间[1,2]上都是减函数,则a的取值范围是
A. | B. |
C. | D. |
设 、
、 分别是定义在
分别是定义在 上的奇函数和偶函数,当
上的奇函数和偶函数,当 时,
时, ,且
,且 ,则不等式
,则不等式 的解集是( )
的解集是( )
A. | B. |
C. | D. |
已知函数y=f(x)在(0,2)上是增函数,函数f(x+2)是偶函数,则
A. | B. |
C. | D. |
已知函数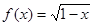 定义域为
定义域为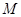 ,
,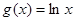 定义域为
定义域为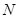 ,则
,则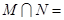 ( )
( )
A.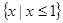 | B.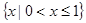 | C.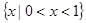 | D.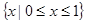 |
函数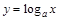 (
(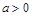 且
且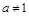 )的图象经过点
)的图象经过点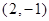 ,函数
,函数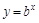 (
(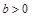 且
且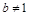 )的图象经过点
)的图象经过点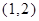 ,则下列关系式中正确的是( )
,则下列关系式中正确的是( )
A.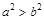 | B.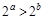 | C.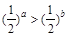 | D.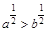 |
函数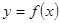 满足
满足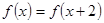 且
且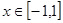 时,
时,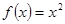 ,则
,则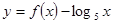 的零点个数为( )
的零点个数为( )
A.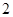 | B.3 | C. 4 | D.5 |
 的图象的大致形状是
的图象的大致形状是