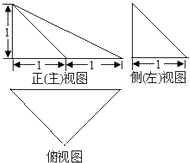
题目内容
【题目】如图,经过村庄A有两条互相垂直的笔直公路AB和AC,根据规划拟在两条公路围成的直角区域内建一工厂P,为了仓库存储和运输方便,在两条公路上分别建两个仓库M,N(异于村庄A,将工厂P及仓库M,N近似看成点,且M,N分别在射线AB,AC上),要求MN=2,PN=1(单位:km),PN⊥MN. 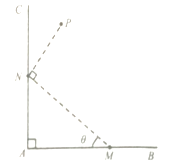
(1)设∠AMN=θ,将工厂与村庄的距离PA表示为θ的函数,记为l(θ),并写出函数l(θ)的定义域;
(2)当θ为何值时,l(θ)有最大值?并求出该最大值.
【答案】
(1)解:过点P作PD⊥AC,垂足为D,连结PA.
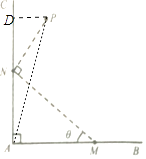
在Rt△MAN中,sinθ= ![]() =
= ![]() ,故NA=2sinθ,
,故NA=2sinθ,
在Rt△PND中,∠PND=θ,sinθ= ![]() =
= ![]() ,cosθ=
,cosθ= ![]() =
= ![]() ,
,
故PD=sinθ,ND=cosθ.
在Rt△PDA中,PA= ![]() =
= ![]()
= ![]() ,
,
所以l(θ)= ![]() ,
,
函数l(θ)的定义域为(0, ![]() ).
).
(2)解:由(1)可知,l(θ)= ![]() ,
,
即l(θ)= ![]() =
= ![]()
= ![]() =
= ![]() =
= 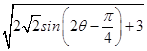 ,
,
又θ∈(0, ![]() ),故2θ﹣
),故2θ﹣ ![]() ∈(﹣
∈(﹣ ![]() ,
, ![]() ),所以当2θ﹣
),所以当2θ﹣ ![]() =
= ![]() ,
,
即θ= ![]() 时,sin(2θ﹣
时,sin(2θ﹣ ![]() )取最大值1,
)取最大值1,
l(θ)max= ![]() =1+
=1+ ![]() .
.
答:当θ= ![]() 时,l(θ)有最大值,最大值为1+
时,l(θ)有最大值,最大值为1+ ![]() .
.
【解析】(1)过点P作PD⊥AC,垂足为D,连结PA.运用直角三角形中锐角三角函数的定义,求得PD,ND,PA;(2)运用同角的平方关系和二倍角公式及两角和差函数公式,化简函数式,再由正弦函数的图形和性质,可得最大值.
【考点精析】认真审题,首先需要了解函数的最值及其几何意义(利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值).

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目