题目内容
【题目】如图,在各棱长均为2的三棱柱![]() 中,侧面
中,侧面![]() 底面ABC,
底面ABC,![]() .
.
(1)求侧棱![]() 与平面
与平面![]() 所成角的正弦值的大小;
所成角的正弦值的大小;
(2)已知点D满足![]() ,在直线
,在直线![]() 上是否存在点P,使DP∥平面
上是否存在点P,使DP∥平面![]() ?若存在,请确定点P的位置,若不存在,请说明理由.
?若存在,请确定点P的位置,若不存在,请说明理由.

【答案】(1)![]() (2)恰好为
(2)恰好为![]() 点.
点.
【解析】
(1)建立空间直角坐标系,求出AA1向量,平面AA1C1C的法向量,然后求出侧棱AA1与平面AB1C所成角的正弦值的大小;
(2)在(1)的前提下,求出![]() ,设出P的坐标,使DP∥平面AB1C,即
,设出P的坐标,使DP∥平面AB1C,即![]() 与法向量共线,再求出P的坐标.
与法向量共线,再求出P的坐标.
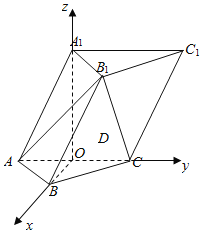
(1)∵侧面![]() 底面ABC,作A1O⊥AC于点O,
底面ABC,作A1O⊥AC于点O,
∴![]() 平面
平面![]() .
.
又![]() ,且各棱长都相等,
,且各棱长都相等,
∴![]() ,
,![]() ,
,![]() .
.
故以O为坐标原点,建立如图所示的空间直角坐标系O-xyz,
则![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() .
.
设平面![]() 的法向量为
的法向量为![]()
则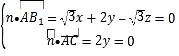 ,取
,取![]() ,得
,得![]() .
.
设侧棱AA1与平面AB1C所成角的为θ,
则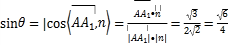 ,
,
∴侧棱![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.
(2)∵![]() ,而
,而![]() ,
,
∴![]() ,又∵
,又∵![]() ,∴点
,∴点![]() .
.
假设存在点P符合题意,则点P的坐标可设为![]() ,∴
,∴![]()
∵DP∥平面![]() ,
,![]() 为平面
为平面![]() 的法向量,∴
的法向量,∴![]() ,得z=
,得z=![]() ,
,
又由![]() ,得
,得![]() ,∴
,∴![]() .
.
又![]() 平面
平面![]() ,故存在点P,使DP∥平面
,故存在点P,使DP∥平面![]() ,其坐标为
,其坐标为![]() ,
,
即恰好为![]() 点.
点.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目




