题目内容
【题目】F1,F2是椭圆C1和双曲线C2的公共焦点,e1,e2分别为曲线C1,C2的离心率,P为曲线C1,C2的一个公共点,若![]() ,且
,且![]() ,则e1∈_____.
,则e1∈_____.
【答案】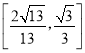 .
.
【解析】
不妨设点P在第一象限,设|PF1|=m,|PF2|=n,在△PF1F2中,由余弦定理可得:4c2=m2+n2﹣2mncos![]() .4c2=a2+3a12得到
.4c2=a2+3a12得到![]() ,根据范围得到答案.
,根据范围得到答案.
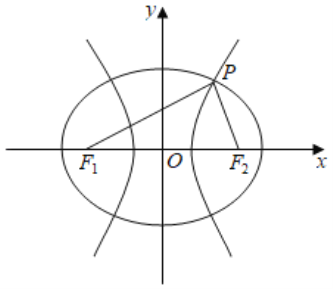
如图所示,设双曲线C2的标准方程为:![]() 1(a1,b1>0),半焦距为c.
1(a1,b1>0),半焦距为c.
椭圆C1:![]() (a>b>0),半焦距为c.
(a>b>0),半焦距为c.
不妨设点P在第一象限,设|PF1|=m,|PF2|=n.
∴m+n=2a,m﹣n=2a1.m=a+a1.n=a﹣a1.
在△PF1F2中,由余弦定理可得:4c2=m2+n2﹣2mncos![]() .4c2=a2+3a12.
.4c2=a2+3a12.
两边同除以c2,得![]() ,∵
,∵![]() ,∴
,∴![]()
∴ .
.
故答案为: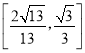

练习册系列答案
相关题目