题目内容
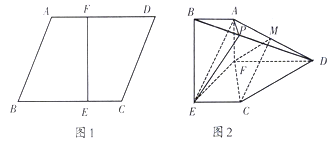
【题目】如图，在矩形ABCD中，
，E为AB的中点．将
沿DE翻折，得到四棱锥
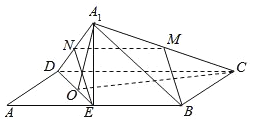
．设
的中点为M，在翻折过程中，有下列三个命题：
①总有
平面
；
②线段BM的长为定值；
③存在某个位置，使DE与所成的角为90°．
其中正确的命题是_______．（写出所有正确命题的序号）
【答案】①②
【解析】
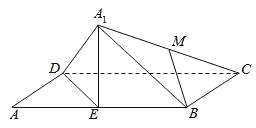
取
D的中点N，连接MN，EN，根据四边形MNEB为平行四边形判断①，②，假设DE⊥C得出矛盾结论判断③．
取D的中点N，连接MN，EN，
则MN为△CD的中位线，
∴MN∥
CD，且MN=CD
又E为矩形ABCD的边AB的中点，∴BE∥CD，且BE=CD
∴MN∥BE，且MN=BE即四边形MNEB为平行四边形，∴BM∥EN，
又EN平面A1DE，BM平面A1DE，
∴BM∥平面DE，故①正确；
由四边形MNEB为平行四边形可得BM＝NE，
而在翻折过程中，NE的长度保持不变，故BM的长为定值，故②正确；
取DE的中点O，连接O，CO，
由D＝E可知O⊥DE，
若DE⊥C，则DE⊥平面OC，
∴DE⊥OC，又∠CDO＝90°﹣∠ADE＝45°，
∴△OCD为等腰直角三角形，故而CD
OD，
而OD
DE，CD＝4，与CDOD矛盾，故DE与C所成的角不可能为90°．
故③错误．
故答案为：①②．
练习册系列答案
名校课堂系列答案
相关题目
