题目内容

6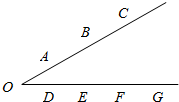．如图，A，B，C三点与D，E，F，G四点分别在一个以O为顶点的角的不同的两边上，则在A，B，C，D，E，F，G，O这8个点中任选三个点作为三角形的三个顶点，可构成的三角形的个数为42．

分析 用间接法，首先计算从A，B，C，D，E，F，G，O中任取3点的情况数目，再计算其中不能构成三角形，即取出的三点在同一条直线上的情况数目，由事件之间的关系，计算可得答案

解答 解：根据题意，从A，B，C，D，E，F，G，O中任取3点，有C83=56种情况，
其中不能构成三角形，即取出的三点在同一条直线上的有C53+C43=14种；
则可以构成三角形的数目为56-14=42；
故答案为：42．

点评 本题考查排列、组合的简单应用，考查学生分析解决问题的能力，属于基础题．

练习册系列答案
相关题目
16．已知（a+1）x-1-lnx≤0对于任意$x∈[{\frac{1}{2}，2}]$恒成立，则a的最大值为（　　）
A．0B．1C．1-2ln2D．$\frac{-1+ln2}{2}$
17．数列{an}中，a1=-$\frac{2}{3}$，当n＞1，n∈N*时，Sn+$\frac{1}{{S}_{n}}$=an-2
（1）求S1，S2，S3的值；
（2）猜想Sn的表达式，并证明你的猜想．
14．将下面三段论形式补充完整：
因为三角函数是周期函数，（大前提）
而y=cosx（x∈R）是三角函数，（小前提）
所以y=cos x （x∈R）是周期函数．（结论）
1．数列{an}的通项公式an=cos$\frac{nπ}{2}$，其前n项和为Sn，则S2015等于-1．
11．已知数列{an}的前n项和Sn，且满足2Sn=nan+3n，（n∈N*）且S2=8．
（1）求a1，a2，a3的值；
（2）证明数列{an}是等差数列，并求数列{an}的通项公式；
（3）求证：$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$+$\frac{1}{{S}_{3}}$+…+$\frac{1}{{S}_{n}}$＜$\frac{3}{4}$．
18．在锐角△ABC中，角A，B，C所对的边分别为a，b，c，已知向量$\overrightarrow{m}$=（sinA，$\frac{1}{2}$），$\overrightarrow{n}$=（3，sinA+$\sqrt{3}$cosA），且$\overrightarrow m$∥$\overrightarrow n$，
（1）求角A的大小；
（2）求$\frac{b+c}{a}$的取值范围．
15．已知函数$f（x）={log_{\frac{1}{2}}}（{{x^2}-ax+1}）$，若函数的定义域为R，则实数a∈（-2，2）；若f（x）的值域为R，则实数a∈（-∞，-2]∪[2，+∞）．
16．命题“对任意x＞0，都有2x＞1”的否定是存在x＞0，有2x≤1．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网