题目内容
18.在锐角△ABC中,角A,B,C所对的边分别为a,b,c,已知向量$\overrightarrow{m}$=(sinA,$\frac{1}{2}$),$\overrightarrow{n}$=(3,sinA+$\sqrt{3}$cosA),且$\overrightarrow m$∥$\overrightarrow n$,(1)求角A的大小;
(2)求$\frac{b+c}{a}$的取值范围.
分析 (1)运用向量共线的坐标表示和三角函数的恒等变换,化简整理即可得到A的值;
(2)运用正弦定理和两角和差的正弦公式,结合锐角三角形和正弦函数的单调性,计算即可得到所求范围.
解答 解:(1)由向量$\overrightarrow{m}$=(sinA,$\frac{1}{2}$),$\overrightarrow{n}$=(3,sinA+$\sqrt{3}$cosA),且$\overrightarrow m$∥$\overrightarrow n$,
$sinA(sinA+\sqrt{3}cosA)=\frac{3}{2}$,即有sin2A+$\sqrt{3}$sinAcosA=$\frac{3}{2}$,
即$\frac{1-cos2A}{2}$+$\frac{\sqrt{3}sin2A}{2}$=$\frac{3}{2}$,
∴$sin(2A-\frac{π}{6})=1$,
∵$A∈(0,\frac{π}{2})$,
∴$2A-\frac{π}{6}∈(-\frac{π}{6},\frac{5π}{6})$,
∴$2A-\frac{π}{6}=\frac{π}{2}$,∴$A=\frac{π}{3}$;
(2)$\frac{b+c}{a}=\frac{sinB+sinC}{sinA}=\frac{{2\sqrt{3}}}{3}[sinB+sin(B+\frac{π}{3})]=2sin(B+\frac{π}{6})$,
$\left\{\begin{array}{l}{0<B<\frac{π}{2}}\\{0<\frac{2π}{3}-B<\frac{π}{2}}\end{array}\right.$⇒$\frac{π}{6}$<B<$\frac{π}{2}$
$⇒B+\frac{π}{6}∈(\frac{π}{3},\frac{2π}{3})$$⇒sin(B+\frac{π}{6})∈(\frac{{\sqrt{3}}}{2},1]⇒\frac{b+c}{a}∈(\sqrt{3},2]$.
点评 本题考查向量共线的坐标表示,二倍角公式和两角和差的正弦公式,正弦函数的性质的运用,同时考查正弦定理的运用,属于中档题.

 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案| A. | $\overrightarrow{e_1}=(0,0),\overrightarrow{e_2}=(2,3)$ | B. | $\overrightarrow{e_1}=(-1,3),\overrightarrow{e_2}=(5,-2)$ | ||
| C. | $\overrightarrow{e_1}=(3,4),\overrightarrow{e_2}=(6,8)$ | D. | $\overrightarrow{e_1}=(2,-3),\overrightarrow{e_2}=(-2,3)$ |
| A. | 相交 | B. | 内切 | C. | 内含 | D. | 外切 |
 正方形ABCD与正方形ABEF互相垂直,点M,N,G分别是AE,BC,CE的中点,AB=2.
正方形ABCD与正方形ABEF互相垂直,点M,N,G分别是AE,BC,CE的中点,AB=2.
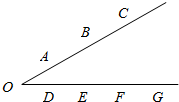 如图,A,B,C三点与D,E,F,G四点分别在一个以O为顶点的角的不同的两边上,则在A,B,C,D,E,F,G,O这8个点中任选三个点作为三角形的三个顶点,可构成的三角形的个数为42.
如图,A,B,C三点与D,E,F,G四点分别在一个以O为顶点的角的不同的两边上,则在A,B,C,D,E,F,G,O这8个点中任选三个点作为三角形的三个顶点,可构成的三角形的个数为42.