题目内容
1.数列{an}的通项公式an=cos$\frac{nπ}{2}$,其前n项和为Sn,则S2015等于-1.分析 由题意可得数列为周期为4的周期数列,计算前4项的值可得.
解答 解:∵$\frac{2π}{\frac{π}{2}}$=4,∴函数y=cos$\frac{πx}{2}$的周期为4,
∴数列an=cos$\frac{nπ}{2}$为周期为4的周期数列,
计算可得a1=0,a2=-1,a3=0,a4=1,
∴S2015=503×(0-1+0+1)+(0-1+0)=-1
故答案为:-1.
点评 本题考查数列求和,涉及数列的周期性,属基础题.

练习册系列答案
相关题目
11.下列结构图中,框①、②处理该分别填入( )


| A. | l?α,l⊥α | B. | l?α,l与α相交 | C. | l?α,l⊥α | D. | l?α,l与α相交 |
13.在下列向量组中,能作为向量基底的是( )
| A. | $\overrightarrow{e_1}=(0,0),\overrightarrow{e_2}=(2,3)$ | B. | $\overrightarrow{e_1}=(-1,3),\overrightarrow{e_2}=(5,-2)$ | ||
| C. | $\overrightarrow{e_1}=(3,4),\overrightarrow{e_2}=(6,8)$ | D. | $\overrightarrow{e_1}=(2,-3),\overrightarrow{e_2}=(-2,3)$ |
10.已知圆O1:(x-1)2+(y+3)2=4,圆O2:(x-2)2+(y+1)2=1,则两圆的位置关系是( )
| A. | 相交 | B. | 内切 | C. | 内含 | D. | 外切 |
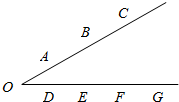 如图,A,B,C三点与D,E,F,G四点分别在一个以O为顶点的角的不同的两边上,则在A,B,C,D,E,F,G,O这8个点中任选三个点作为三角形的三个顶点,可构成的三角形的个数为42.
如图,A,B,C三点与D,E,F,G四点分别在一个以O为顶点的角的不同的两边上,则在A,B,C,D,E,F,G,O这8个点中任选三个点作为三角形的三个顶点,可构成的三角形的个数为42.