题目内容
11.已知数列{an}的前n项和Sn,且满足2Sn=nan+3n,(n∈N*)且S2=8.(1)求a1,a2,a3的值;
(2)证明数列{an}是等差数列,并求数列{an}的通项公式;
(3)求证:$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$+$\frac{1}{{S}_{3}}$+…+$\frac{1}{{S}_{n}}$<$\frac{3}{4}$.
分析 (1)由2S1=a1+3求a1,再求a2,a3的值;
(2)先由2Sn=nan+3n得到an=$\frac{n-1}{n-2}$an-1-$\frac{3}{n-2}$,从而由数学归纳法证明,再写出通项公式;
(3)化简Sn=$\frac{3+2n+1}{2}$n=n(n+2),从而求得$\frac{1}{{S}_{n}}$=$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),从而求前n项和即可.
解答 解:(1)由题意得,2S1=a1+3,则2a1=a1+3,a1=3;
又∵S2=a1+a2=8,∴a2=5,
2S3=3a3+3×3,解得,a3=7;
(2)当n≥3时,∵2Sn=nan+3n,①
2Sn-1=(n-1)an-1+3(n-1),②
①-②得,2an=nan-(n-1)an-1+3,整理得an=$\frac{n-1}{n-2}$an-1-$\frac{3}{n-2}$,
∵a1=3,a2=5,a3=7;
∴猜想an=2n+1,证明如下,
当n=1,2,3时,显然成立;
当n≥3时,假设an=2n+1成立,
则an+1=$\frac{n}{n-1}$an-$\frac{3}{n-1}$=$\frac{n}{n-1}$(2n+1)-$\frac{3}{n-1}$=2n+3=2(n+1)+1,
综上所述,an=2n+1;
故数列{an}是等差数列,且数列{an}的通项公式an=2n+1;
(3)证明:由(2)知,Sn=$\frac{3+2n+1}{2}$n=n(n+2),可得$\frac{1}{{S}_{n}}$=$\frac{1}{n(n+2)}$=$\frac{1}{2}$($\frac{1}{n}$-$\frac{1}{n+2}$),
则$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$+$\frac{1}{{S}_{3}}$+…+$\frac{1}{{S}_{n}}$
=$\frac{1}{2}$[(1-$\frac{1}{3}$)+($\frac{1}{2}$-$\frac{1}{4}$)+($\frac{1}{3}$-$\frac{1}{5}$)+…+($\frac{1}{n-1}$-$\frac{1}{n+1}$)+($\frac{1}{n}$-$\frac{1}{n+2}$)]
=$\frac{1}{2}$(1+$\frac{1}{2}$-$\frac{1}{n+1}$-$\frac{1}{n+2}$)
=$\frac{3}{4}$-$\frac{1}{2}$($\frac{1}{n+1}$+$\frac{1}{n+2}$)<$\frac{3}{4}$.
点评 本题考查了数列的通项公式的求法与数列证明,同时考查了前n项和的求法及数学归纳法的应用,属于难题.

| A. | 3$\sqrt{3}$ | B. | 1 | C. | $\sqrt{3}$ | D. | 3 |
| A. | $\frac{13}{16}$ | B. | $\frac{4}{243}$ | C. | $\frac{13}{243}$ | D. | $\frac{80}{243}$ |
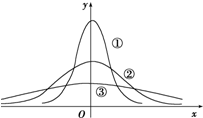 图是三个正态分布X~N(0,0.01),Y~N(0,1),Z~N(0,2.25)的密度曲线,则三个随机变量X,Y,Z对应曲线分别是图中的①、②、③.
图是三个正态分布X~N(0,0.01),Y~N(0,1),Z~N(0,2.25)的密度曲线,则三个随机变量X,Y,Z对应曲线分别是图中的①、②、③.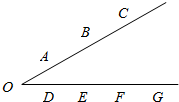 如图,A,B,C三点与D,E,F,G四点分别在一个以O为顶点的角的不同的两边上,则在A,B,C,D,E,F,G,O这8个点中任选三个点作为三角形的三个顶点,可构成的三角形的个数为42.
如图,A,B,C三点与D,E,F,G四点分别在一个以O为顶点的角的不同的两边上,则在A,B,C,D,E,F,G,O这8个点中任选三个点作为三角形的三个顶点,可构成的三角形的个数为42.