题目内容
10.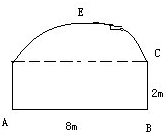 某工程设计一条单行隧道,其横截面如图所示,下部ABCD为长8米高2米的矩形,上部$\widehat{CED}$是圆弧的一部分,欲使宽6米高3米的大型货车刚好能通过,求拱顶E距离路面AB至少需几米?
某工程设计一条单行隧道,其横截面如图所示,下部ABCD为长8米高2米的矩形,上部$\widehat{CED}$是圆弧的一部分,欲使宽6米高3米的大型货车刚好能通过,求拱顶E距离路面AB至少需几米?
分析 建立以AB的中点为坐标原点和AB所在直线为x轴的直角坐标系.由图可知,C(4,2),G(3,3),D(-4,2)
设圆弧$\widehat{CED}$的方程为:x2+y2+Dx+Ey+F=0(D2+E2-4F>0),代入点的坐标,得到方程,解方程可得圆方程,再令x=0,解得y,即为所求.
解答 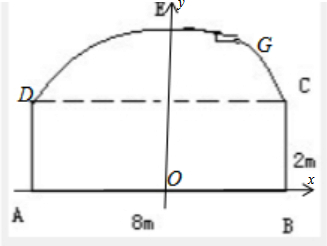 解:建立以AB的中点为坐标原点和AB所在直线为x轴的直角坐标系.
解:建立以AB的中点为坐标原点和AB所在直线为x轴的直角坐标系.
由图可知,C(4,2),G(3,3),D(-4,2)
设圆弧$\widehat{CED}$的方程为:x2+y2+Dx+Ey+F=0
(D2+E2-4F>0)
将C,G,D三点坐标代入,可得$\left\{\begin{array}{l}{4D+2E+F=-20}\\{-4D+2E+F=-20}\\{3D+3E+F=-18}\end{array}\right.$,
解得D=0,E=2,F=-24.
即有圆方程为:x2+y2+2y-24=0,
令x=0,解出y=4或-6(舍去),
因此OE=4.
答:拱顶E距离路面AB至少需4米.
点评 本题考查圆的方程的求法和运用,注意运用待定系数法,考查运算求解能力,属于中档题.

练习册系列答案
 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案
相关题目
20.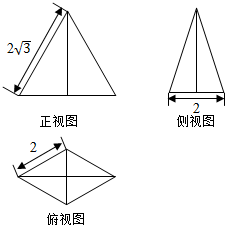 如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是边长为2$\sqrt{3}$的等边三角形,底边长为2的等腰三角形和菱形,则该几何体体积为( )
如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是边长为2$\sqrt{3}$的等边三角形,底边长为2的等腰三角形和菱形,则该几何体体积为( )
 如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是边长为2$\sqrt{3}$的等边三角形,底边长为2的等腰三角形和菱形,则该几何体体积为( )
如图,某几何体的正视图(主视图),侧视图(左视图)和俯视图分别是边长为2$\sqrt{3}$的等边三角形,底边长为2的等腰三角形和菱形,则该几何体体积为( )| A. | 2$\sqrt{3}$ | B. | 4 | C. | 4$\sqrt{3}$ | D. | 2 |