题目内容
17.已知实数x,y满足x2+y2≤1,则(1)(x+2)2+(y-2)2的最小值是9-4$\sqrt{2}$;
(2)|2x+y-4|+|6-x-3y|的最大值是15.
分析 (1)画出x2+y2≤1表示的平面区域,可得单位圆面,(x+2)2+(y-2)2的几何意义为单位圆面内的点与A(-2,2)的距离的平方,连接AO,与圆的交点即为所求;
(2)由于-1≤x≤1,-1≤y≤1,可去掉绝对值可得10-3x-4y,设10-3x-4y=t,当直线3x+4y+t-10=0与圆x2+y2=1相切时,t取得最值,计算即可得到所求最大值.
解答 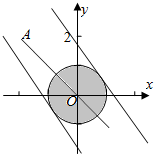 解:(1)画出x2+y2≤1表示的平面区域,
解:(1)画出x2+y2≤1表示的平面区域,
可得单位圆面,(x+2)2+(y-2)2的几何意义为
单位圆面内的点与A(-2,2)的距离的平方,
连接AO,与圆的交点即为所求,可得最小值为
(|AO|-1)2=($\sqrt{4+4}$-1)2=9-4$\sqrt{2}$;
(2)由于-1≤x≤1,-1≤y≤1,
可得-3≤2x+y≤3,-4≤x+3y≤4,
则|2x+y-4|+|6-x-3y|=4-2x-y+6-x-3y=10-3x-4y,
设10-3x-4y=t,当直线3x+4y+t-10=0与圆x2+y2=1相切时,t取得最值.
由相切的条件:d=r,即为$\frac{|t-10|}{\sqrt{{3}^{2}+{4}^{2}}}$=1,解得t=5或15.
故最大值为15.
故答案为:9-4$\sqrt{2}$,15.
点评 本题考查直线与圆的位置关系,注意运用圆外一点和圆上的点的距离的最大值为d+r,最小值为d-r,以及直线和圆相切的条件:d=r,考查运算能力,属于中档题.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
7.已知抛物线M:y2=4x,圆N:(x-1)2+y2=r2(其中r为常数,r>0).过点(1,0)的直线l交圆N于C、D两点,交抛物线M于A、B两点,且满足|AC|=|BD|的直线l只有三条的必要不充分条件是( )
| A. | r∈(0,1] | B. | r∈(1,2] | C. | r∈[$\sqrt{3}$,4) | D. | r∈[ln2,+∞) |
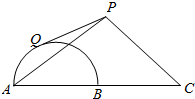 在如图所示的平面中,点C为半圆的直径AB延长线上的一点,AB=BC=2,过动点P作半圆的切线PQ,若PC=$\sqrt{2}$PQ,则△PAC的面积的最大值为4$\sqrt{5}$.
在如图所示的平面中,点C为半圆的直径AB延长线上的一点,AB=BC=2,过动点P作半圆的切线PQ,若PC=$\sqrt{2}$PQ,则△PAC的面积的最大值为4$\sqrt{5}$.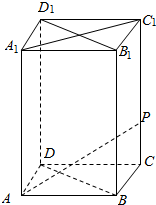 如图,在底面边长为1,侧棱长为2的正四棱柱ABCDA1B1C1D1中,P是侧棱CC1上的一点,CP=1,求异面直线AP与BD1所成角的余弦.
如图,在底面边长为1,侧棱长为2的正四棱柱ABCDA1B1C1D1中,P是侧棱CC1上的一点,CP=1,求异面直线AP与BD1所成角的余弦.