题目内容
2.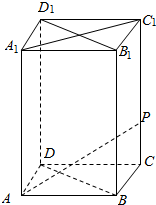 如图,在底面边长为1,侧棱长为2的正四棱柱ABCDA1B1C1D1中,P是侧棱CC1上的一点,CP=1,求异面直线AP与BD1所成角的余弦.
如图,在底面边长为1,侧棱长为2的正四棱柱ABCDA1B1C1D1中,P是侧棱CC1上的一点,CP=1,求异面直线AP与BD1所成角的余弦.
分析 以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出异面直线AP与BD1所成角的余弦值.
解答  解:∵在底面边长为1,侧棱长为2的正四棱柱ABCDA1B1C1D1中,
解:∵在底面边长为1,侧棱长为2的正四棱柱ABCDA1B1C1D1中,
P是侧棱CC1上的一点,CP=1,
∴以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,
则A(1,0,0),P(0,1,1),B(1,1,0),D1(0,0,2),
$\overrightarrow{AP}$=(-1,1,1),$\overrightarrow{B{D}_{1}}$=(-1,-1,2),
设异面直线AP与BD1所成角为θ,
则cosθ=|$\frac{\overrightarrow{AP}•\overrightarrow{B{D}_{1}}}{|\overrightarrow{AP}|•|\overrightarrow{B{D}_{1}}|}$|=|$\frac{1-1+2}{\sqrt{3}•\sqrt{6}}$|=$\frac{\sqrt{2}}{3}$.
∴异面直线AP与BD1所成角的余弦值为$\frac{\sqrt{2}}{3}$.
点评 本题考查异面直线所成角的余弦值的求法,是基础题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目