题目内容
5.若F1,F2是双曲线$\frac{x^2}{9}-\frac{y^2}{16}=1$的两个焦点,P是双曲线上的一点,且|PF1|•|PF2|=64,则∠F1PF2=$\frac{π}{3}$.分析 由双曲线方程求出焦距,利用双曲线的定义和余弦定理能求出∠F1PF2.
解答 解:由$\frac{x^2}{9}-\frac{y^2}{16}=1$,得a2=9,b2=16,∴c=5,
∴|F1F2|=2c=10,
设|PF1|>|PF2|,
则|PF1|-|PF2|=6,
∴$|P{F}_{1}{|}^{2}+|P{F}_{2}{|}^{2}-2|P{F}_{1}||P{F}_{2}|=36$,
∵|PF1||PF2|=64,
∴$|P{F}_{1}{|}^{2}+|P{F}_{2}{|}^{2}=164$,
∴cos∠F1PF2=$\frac{|P{F}_{1}{|}^{2}+|P{F}_{2}{|}^{2}-|{F}_{1}{F}_{2}{|}^{2}}{2|P{F}_{1}||P{F}_{2}|}$=$\frac{164-100}{2×64}=\frac{1}{2}$,
∴∠F1PF2=$\frac{π}{3}$.
故答案为:$\frac{π}{3}$.
点评 本题考查双曲线是几何性质,考查双曲线的定义,注意余弦定理的合理运用,是中档题.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
15.函数y=f(x)满足对任意x1,x2∈[0,2](x1≠x2),$\frac{f({x}_{2})-f({x}_{1})}{{x}_{2}-{x}_{1}}$>0,且函数f(x+2)是偶函数,则下列结论成立的是( )
| A. | f(1)<f($\frac{5}{2}$)<f($\frac{7}{2}$) | B. | f($\frac{7}{2}$)<f(1)<f($\frac{5}{2}$) | C. | f($\frac{7}{2}$)<f($\frac{5}{2}$)<f(1) | D. | f($\frac{5}{2}$)<f(1)<f($\frac{7}{2}$) |
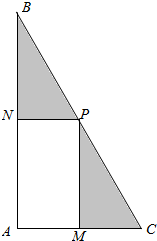 我校为进行“阳光运动一小时”活动,计划在一块直角三角形ABC的空地上修建一个占地面积为S(平方米)的矩形AMPN健身场地.如图,点M在AC上,点N在AB上,且P点在斜边BC上.已知∠ACB=60°,|AC|=30米,|AM|=x米,x∈[10,20].设矩形AMPN健身场地每平方米的造价为$\frac{37k}{{\sqrt{S}}}$元,再把矩形AMPN以外(阴影部分)铺上草坪,每平方米的造价为$\frac{12k}{{\sqrt{S}}}$元(k为正常数).
我校为进行“阳光运动一小时”活动,计划在一块直角三角形ABC的空地上修建一个占地面积为S(平方米)的矩形AMPN健身场地.如图,点M在AC上,点N在AB上,且P点在斜边BC上.已知∠ACB=60°,|AC|=30米,|AM|=x米,x∈[10,20].设矩形AMPN健身场地每平方米的造价为$\frac{37k}{{\sqrt{S}}}$元,再把矩形AMPN以外(阴影部分)铺上草坪,每平方米的造价为$\frac{12k}{{\sqrt{S}}}$元(k为正常数).