题目内容
【题目】已知下列命题:( )
①向量 ![]() ,
, ![]() 不共线,则向量
不共线,则向量 ![]() 与向量
与向量 ![]() 一定不共线
一定不共线
②对任意向量 ![]() ,
, ![]() ,则
,则 ![]() 恒成立
恒成立
③在同一平面内,对两两均不共线的向量 ![]() ,
, ![]() ,
, ![]() ,若给定单位向量
,若给定单位向量 ![]() 和正数
和正数 ![]() ,总存在单位向量
,总存在单位向量 ![]() 和实数
和实数 ![]() ,使得
,使得 ![]()
则正确的序号为( )
A.①②③
B.①③
C.②③
D.①②
【答案】D
【解析】对于①,假设向量 ![]() 与向量
与向量 ![]() 共线,故存在常数
共线,故存在常数 ![]() 使得
使得 ![]() 成立,即
成立,即 ![]() ,由于向量
,由于向量 ![]() ,
, ![]() 不共线,故
不共线,故 ![]() 无解,故假设不成立,即向量
无解,故假设不成立,即向量 ![]() 与向量
与向量 ![]() 一定不共线,故①正确;
一定不共线,故①正确; ![]() ,
, ![]() ,由于
,由于 ![]() ,故
,故 ![]() 恒成立,即②正确;对于③,取
恒成立,即②正确;对于③,取 ![]() ,
, ![]() ,
, ![]() ,无论
,无论 ![]() 取何值,向量
取何值,向量 ![]() 都平行于
都平行于 ![]() 轴,而向量
轴,而向量 ![]() 的模恒等于
的模恒等于 ![]() ,要使
,要使 ![]() 成立,根据平行四边形法则,向量
成立,根据平行四边形法则,向量 ![]() 的纵坐标一定为4,故找不到这样的单位向量
的纵坐标一定为4,故找不到这样的单位向量 ![]() 使等式成立,故③错误; 故答案为:D.
使等式成立,故③错误; 故答案为:D.
由向量共线的性质定理即可得出①正确,再由向量的数量积运算公式得出②正确,借助向量的线性关系得出③错误。

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】假设某种设备使用的年限x(年)与所支出的维修费用y(元)有以下统计资料:
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
参考数据: ![]() ,
, ![]() ,
,
如果由资料知y对x呈线性相关关系.试求:
(1)![]() ;
;
(2)线性回归方程 ![]() =bx+a.
=bx+a.
(3)估计使用10年时,维修费用是多少?
【题目】某种商品价格与该商品日需求量之间的几组对照数据如表:
价格x(元/kg) | 10 | 15 | 20 | 25 | 30 |
日需求量y(kg) | 11 | 10 | 8 | 6 | 5 |
参考公式:线性回归方程 ![]() ,其中
,其中 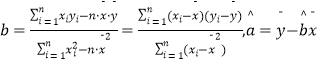 .
.
(1)求y关于x的线性回归方程;
(2)利用(1)中的回归方程,当价格x=40元/kg时,日需求量y的预测值为多少?