Question

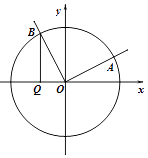
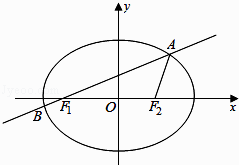
【题目】如图，已知椭圆 的离心率为 ，F1、F2为其左、右焦点，过F1的直线l交椭圆于A、B两点，△F1AF2的周长为 ．
（1）求椭圆的标准方程；
（2）求△AOB面积的最大值（O为坐标原点）．

Answer 1

【答案】
（1）解：设椭圆的半焦距为c，则 ，由题意知 ，

二者联立解得 ，c=1，则b2=1，所以椭圆的标准方程为

（2）解：设直线l的方程为：x=ky﹣1，与 联立，消x，整理得：（k2+2）y2﹣2ky﹣1=0，△=（﹣2k）2+4（k2+2）=8k2+8＞0， ， ，

所以 = = =

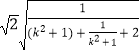
= = = = （当且仅当 ，即k=0时等号成立），所以△AOB面积的最大值为 ．

说明：若设直线l的方程为：y=k（x+1）（k≠0），则 ，与 联立，消x，整理得： ， ，

所以 = = = = ，

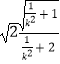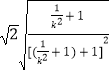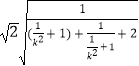
当且仅当 ，即k=0时等号成立，由k≠0，则 ．

当直线l的方程为：x=﹣1时，此时 ， ．

综上所述：△AOB面积的最大值为

【解析】（1）设椭圆的半焦距为c，利用离心率以及△F1AF2的周长，解得a，c，然后求解椭圆的标准方程．（2）设直线l的方程为：x=ky﹣1，与 联立，消x，整理得：（k2+2）y2﹣2ky﹣1=0求出A，B的纵坐标，表示出三角形的面积公式，化简整理，通过基本不等式求出最值．说明：若设直线l的方程为：y=k（x+1）（k≠0），则 ，与 联立，方法与前边的求解相同．
【考点精析】解答此题的关键在于理解椭圆的标准方程的相关知识，掌握椭圆标准方程焦点在x轴：，焦点在y轴：．