题目内容
【题目】2017高考特别强调了要增加对数学文化的考查,为此某校高三年级特命制了一套与数学文化有关的专题训练卷(文、理科试卷满分均为100分),并对整个高三年级的学生进行了测试.现从这些学生中随机抽取了50名学生的成绩,按照成绩为 ![]() ,
, ![]() ,…,
,…, ![]() 分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).
分成了5组,制成了如图所示的频率分布直方图(假定每名学生的成绩均不低于50分).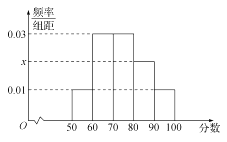
(1)求频率分布直方图中的 ![]() 的值,并估计所抽取的50名学生成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表);
的值,并估计所抽取的50名学生成绩的平均数、中位数(同一组中的数据用该组区间的中点值代表);
(2)若高三年级共有2000名学生,试估计高三学生中这次测试成绩不低于70分的人数;
(3)若利用分层抽样的方法从样本中成绩不低于70分的三组学生中抽取6人,再从这6人中随机抽取3人参加这次考试的考后分析会,试求后两组中至少有1人被抽到的概率.
【答案】
(1)解:由频率分布直方图可得第4组的频率为 ![]()
![]() ,
,
故 ![]() .
.
故可估计所抽取的50名学生成绩的平均数为
![]()
![]()
![]() (分).
(分).
由于前两组的频率之和为 ![]() ,前三组的频率之和为
,前三组的频率之和为 ![]() ,故中位数在第3组中.
,故中位数在第3组中.
设中位数为 ![]() 分,
分,
则有 ![]() ,所以
,所以 ![]() ,
,
即所求的中位数为 ![]() 分
分
(2)解:由(1)可知,50名学生中成绩不低于70分的频率为 ![]() ,
,
由以上样本的频率,可以估计高三年级2000名学生中成绩不低于70分的人数为 ![]()
(3)解:由(1)可知,后三组中的人数分别为15,10,5,故这三组中所抽取的人数分别为3,2,1.记成绩在 ![]() 这组的3名学生分别为
这组的3名学生分别为 ![]() ,
, ![]() ,
, ![]() ,成绩在
,成绩在 ![]() 这组的2名学生分别为
这组的2名学生分别为 ![]() ,
, ![]() ,成绩在
,成绩在 ![]() 这组的1名学生为
这组的1名学生为 ![]() ,则从中任抽取3人的所有可能结果为
,则从中任抽取3人的所有可能结果为 ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() 共20种.
共20种.
其中后两组中没有人被抽到的可能结果为 ![]() ,只有1种,
,只有1种,
故后两组中至少有1人被抽到的概率为 ![]() .
.
【解析】(1)由频率的直方图求出第4组的频率从而得到x的值,进而可估计所抽取的50名学生成绩的平均数和中位数。(2)先求出50名学生中成绩不低于70分的频率为0.6,由此可以估计高三年级2000名学生中成绩不低于70分的人数。(3)由列举法一一列出各个成绩段的满足题意的人数,由概率的定义得到两组中至少有1人被抽到的概率的值。
【考点精析】关于本题考查的频率分布直方图和概率的意义,需要了解频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息;任何事件的概率是0~1之间的一个确定的数,它度量该事情发生的可能性.小概率事件很少发生,而大概率事件则经常发生.知道随机事件的概率有利于我们作出正确的决策才能得出正确答案.

 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程记录的产量 ![]() (吨)与相应的生产能耗
(吨)与相应的生产能耗 ![]() (吨标准煤)的几组对照数据:
(吨标准煤)的几组对照数据:
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |
参考公式: 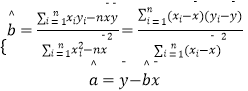
(1)已知产量 ![]() 和能耗
和能耗 ![]() 呈线性关系,请根据上表提供的数据,用最小二乘法求出
呈线性关系,请根据上表提供的数据,用最小二乘法求出 ![]() 关于
关于 ![]() 的线性回归方程
的线性回归方程 ![]() ;
;
(2)已知该厂技改前100吨甲产品的生产耗能为90吨标准煤,试根据(1)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?