题目内容
已知向量 ,
,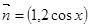 ,
,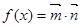 .
.
(Ⅰ)求函数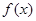 的最小正周期及对称轴方程;
的最小正周期及对称轴方程;
(Ⅱ)在△ABC中,角A,B,C的对边分别是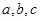 若
若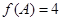 ,b=1,△ABC的面积为
,b=1,△ABC的面积为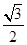 ,求
,求 的值.
的值.
(Ⅰ)最小正周期T=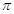 ,对称轴方程为
,对称轴方程为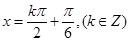 ;(Ⅱ)
;(Ⅱ)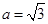 .
.
解析试题分析:(Ⅰ)利用平面向量的坐标运算及三角函数的和差倍半公式,首先化简函数,得到 .明确最小正周期T=
.明确最小正周期T=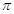 ,对称轴方程为
,对称轴方程为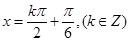 .
.
(Ⅱ)依题意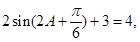 得到
得到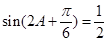 ,结合
,结合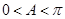 ,推出A=
,推出A=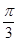 ;
;
根据三角形面积求得c=2,由余弦定理得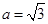 .
.
本题较为典型,将三角函数、平面向量、正余弦定理巧妙地结合在一起 ,对考生能力考查较为全面.
试题解析:
(Ⅰ)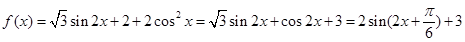 . 4分
. 4分
所以最小正周期T=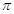 ,对称轴方程为
,对称轴方程为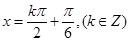 (6分)
(6分)
(Ⅱ)依题意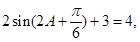 即
即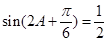 ,由于
,由于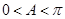 ,
,
所以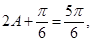 A=
A=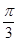 (9分)
(9分)
又∵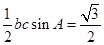 且b=1,∴
且b=1,∴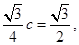 得c=2,在
得c=2,在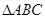 中,由余弦定理得
中,由余弦定理得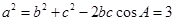 ,所以
,所以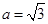 (12分)
(12分)
考点:平面向量的坐标运算,三角函数和差倍半公式,余弦定理的应用.

练习册系列答案
 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
 ,
, ,
,
 ,求
,求 的值;
的值; 中,角
中,角 的对边分别是
的对边分别是 ,且满足
,且满足 ,求函数
,求函数 的取值范围.
的取值范围. ,且
,且 ,
, ,
, 的图象相邻两对称轴之间的距离等于
的图象相邻两对称轴之间的距离等于 .
. 分别为角
分别为角 的对边,
的对边, ,
, ,求△ABC面积的最大值.
,求△ABC面积的最大值. 中,内角
中,内角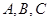 所对边长分别为
所对边长分别为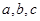 ,
,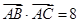 ,
,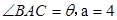 .
.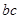 的最大值; (2)求函数
的最大值; (2)求函数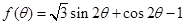 的值域.
的值域.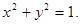 已知BC平行于x轴,AB所在直线方程为
已知BC平行于x轴,AB所在直线方程为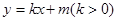 ,记角A,B,C所对的边分别是a,b,c.
,记角A,B,C所对的边分别是a,b,c.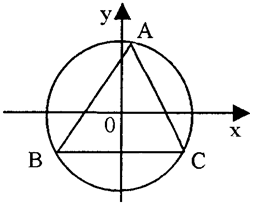
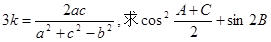 的值;
的值;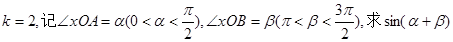 的值.
的值.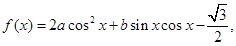 x∈R且
x∈R且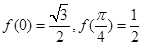 ,
, 的最小正周期;
的最小正周期;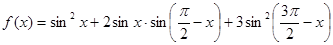
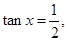 求
求 的值;
的值; ,
,
 的值;
的值; 的最大值和最小值.
的最大值和最小值.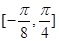 上的值域;
上的值域;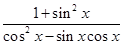 的值.
的值.