题目内容
已知直线 :y="k" (x+2
:y="k" (x+2 )与圆O:
)与圆O: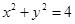 相交于A、B两点,O是坐标原点,
相交于A、B两点,O是坐标原点, ABO的面积为S.
ABO的面积为S.
(1)试将S表示成的函数S(k),并求出它的定义域;
(2)求S的最大值,并求取得最大值时k的值.
 :y="k" (x+2
:y="k" (x+2 )与圆O:
)与圆O: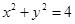 相交于A、B两点,O是坐标原点,
相交于A、B两点,O是坐标原点, ABO的面积为S.
ABO的面积为S.(1)试将S表示成的函数S(k),并求出它的定义域;
(2)求S的最大值,并求取得最大值时k的值.
(1)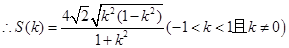
(2) 即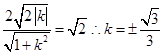 ,
, 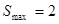 .
.
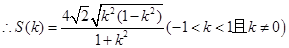
(2) 即
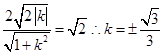 ,
, 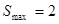 .
.(1)先求出三角形的高,即原点O到直线的距离,然后再利用圆的弦长公式求出三角形的底的长度,进而确定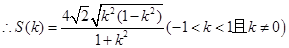
(2)求最值要换元.令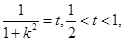
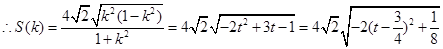 ,这样转化成二次函数最值解决即可.
,这样转化成二次函数最值解决即可.
解:如图,(1)直线 方程为:
方程为: 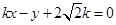 ,且
,且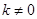 .——————2分
.——————2分
原点O到 的距离为
的距离为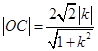 ——————3分
——————3分
弦长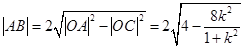 ——————4分
——————4分
△ABO面积 ————————6分
————————6分
△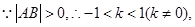
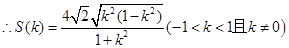 ——————————8分
——————————8分
(2) 令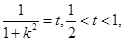 则——————10分
则——————10分
 .————12分
.————12分
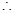 当t=
当t=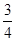 时,
时, 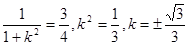 时,
时, 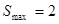 ————————14分
————————14分
另解:△ABO面积S=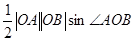
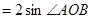
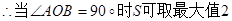 ,此时
,此时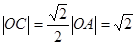
即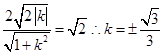 ,所以
,所以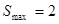 .
.
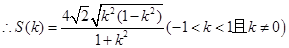
(2)求最值要换元.令
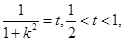
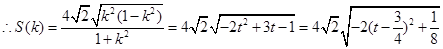 ,这样转化成二次函数最值解决即可.
,这样转化成二次函数最值解决即可.解:如图,(1)直线
 方程为:
方程为: 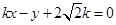 ,且
,且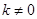 .——————2分
.——————2分原点O到
 的距离为
的距离为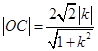 ——————3分
——————3分弦长
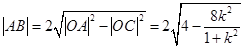 ——————4分
——————4分△ABO面积
 ————————6分
————————6分△
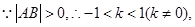
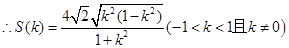 ——————————8分
——————————8分(2) 令
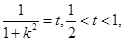 则——————10分
则——————10分 .————12分
.————12分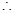 当t=
当t=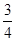 时,
时, 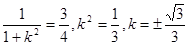 时,
时, 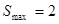 ————————14分
————————14分另解:△ABO面积S=
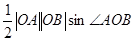
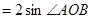
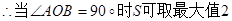 ,此时
,此时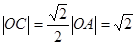
即
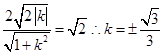 ,所以
,所以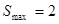 .
.
练习册系列答案
相关题目
 的方程为
的方程为 ,直线
,直线 的方程为
的方程为 ,点
,点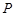 在直线
在直线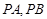 ,切点为
,切点为 .
. ,试求点
,试求点 三点的圆必过定点,并求出所有定点的坐标;
三点的圆必过定点,并求出所有定点的坐标; 长的最小值.
长的最小值.
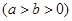 的离心率为
的离心率为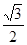 ,直线
,直线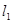 经过椭圆的上顶点
经过椭圆的上顶点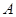 和右顶点
和右顶点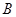 ,并且和圆
,并且和圆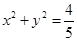 相切.
相切. 的方程;
的方程;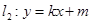
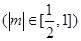 与椭圆
与椭圆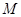 ,
,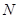 两点,以线段
两点,以线段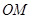 ,
, 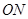 为邻边作平行四边行
为邻边作平行四边行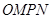 ,其中顶点
,其中顶点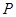 在椭圆
在椭圆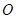 为坐标原点,求
为坐标原点,求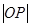 的取值范围.
的取值范围.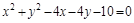 上的点到直线
上的点到直线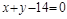 的最大距离与最小距离的差是( )
的最大距离与最小距离的差是( )
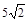
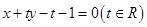 与圆
与圆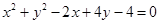 的位置关系为( )
的位置关系为( )
 与圆
与圆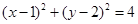 相交于
相交于 、
、 两点,且弦
两点,且弦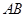 的长为
的长为 ,则
,则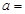 __________.
__________. 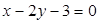 与圆
与圆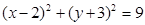 交于E、F两点,则弦长EF=
交于E、F两点,则弦长EF=