题目内容
15. 已知n3(n∈N*)有如下的拆分方式:13=1,23=2+4+2,33=3+6+9+6+3,…,这些通过拆分得到的数可组成右边的数阵:
已知n3(n∈N*)有如下的拆分方式:13=1,23=2+4+2,33=3+6+9+6+3,…,这些通过拆分得到的数可组成右边的数阵:(1)认真观察数阵,求和:13+23+…+n3;
(2)若数列{an}中的每一项都大于0,证明:{an}的通项公式为an=n的充要条件是对任意的n∈N*,都有$\frac{{a}_{1}^{3}+{a}_{2}^{3}+…+{a}_{n}^{3}}{{a}_{1}+{a}_{2}+…+{a}_{n}}$=$\frac{1}{2}$n(n+1).
分析 (1)通过读取图表,可以看出13+23+…+n3可转化为n个等差数列的前n项和,然后由等差数列的前n项和得答案;
(2)证必要性可直接把an=n代入等式左边证明,充分性由等式右边=$\frac{[\frac{1}{2}n(n+1)]^{2}}{\frac{1}{2}n(n+1)}$,再结合(1)证明.
解答 (1)解:由数阵可知,
13+23+…+n3=(1+2+…+n)+2(1+2+…+n)+…+n(1+2+…+n)
=(1+2+…+n)(1+2+…+n)=$[\frac{1}{2}n(n+1)]^{2}$;
(2)证明:必要性:由an=n,得$\frac{{a}_{1}^{3}+{a}_{2}^{3}+…+{a}_{n}^{3}}{{a}_{1}+{a}_{2}+…+{a}_{n}}$=$\frac{[\frac{1}{2}n(n+1)]^{2}}{\frac{1}{2}n(n+1)}=\frac{1}{2}n(n+1)$;
充分性:若数列{an}满足$\frac{{a}_{1}^{3}+{a}_{2}^{3}+…+{a}_{n}^{3}}{{a}_{1}+{a}_{2}+…+{a}_{n}}$=$\frac{1}{2}$n(n+1),
即$\frac{{a}_{1}^{3}+{a}_{2}^{3}+…+{a}_{n}^{3}}{{a}_{1}+{a}_{2}+…+{a}_{n}}$=$\frac{1}{2}$n(n+1)=$\frac{[\frac{1}{2}n(n+1)]^{2}}{\frac{1}{2}n(n+1)}$=$\frac{(1+2+…+n)(1+2+…+n)}{1+2+…+n}$
=$\frac{(1+2+…+n)+2(1+2+…+n)+…+n(1+2+…+n)}{1+2+…+n}$,
由(1)知,$\frac{(1+2+…+n)+2(1+2+…+n)+…+n(1+2+…+n)}{1+2+…+n}$=$\frac{{1}^{3}+{2}^{3}+…+{n}^{3}}{1+2+…+n}$,
∴an=n.
即:若数列{an}中的每一项都大于0,则{an}的通项公式为an=n的充要条件是对任意的n∈N*,都有$\frac{{a}_{1}^{3}+{a}_{2}^{3}+…+{a}_{n}^{3}}{{a}_{1}+{a}_{2}+…+{a}_{n}}$=$\frac{1}{2}$n(n+1).
点评 本题考查了数列的求和,考查了学生读取图表的能力,训练了充分必要条件的证明方法,是中档题.

| A. | 2$\sqrt{5}$ | B. | 2$\sqrt{6}$ | C. | $\sqrt{34}$ | D. | 2$\sqrt{7}$ |
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
| 广告费用x(单位:万元) | 2 | 3 | 4 | 5 |
| 利润y(单位:万元) | 26 | ● | 49 | 54 |
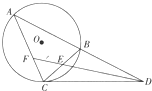 如图所示,已知A、B、C三点都在⊙O上,CD是⊙O的切线,直线AB与CD交于点D.
如图所示,已知A、B、C三点都在⊙O上,CD是⊙O的切线,直线AB与CD交于点D.