题目内容
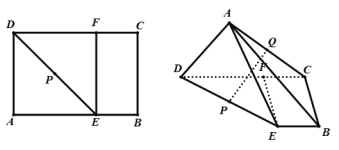
【题目】如图,△ABC和△BCD所在平面互相垂直,且AB=BC=BD=2,∠ABC=∠DBC=120°,E,F分别为AC,DC的中点.
(1)求证:EF⊥BC;
(2)求二面角E-BF-C的正弦值.

【答案】(1)见解析(2)![]()
【解析】
(1)先证明BC⊥平面EFO,即证EF⊥BC.(2)利用向量法求二面角E-BF-C的正弦值.
(1)证明:如图,过E作EO⊥BC,垂足为O,连接OF,
由题意得△ABC≌△DBC,可证出△EOC≌△FOC,
所以∠EOC=∠FOC=![]() ,即FO⊥BC,
,即FO⊥BC,
又EO⊥BC,EO∩FO=O,
因此BC⊥平面EFO.又EF平面EFO,
所以EF⊥BC.
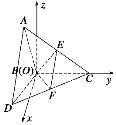
(2)证明:由题意,以B为坐标原点,在平面DBC内过B作垂直于BC的直线为x轴,BC所在直线为y轴,在平面ABC内过B作垂直BC的直线为z轴,建立如图所示的空间直角坐标系,易得B(0,0,0),A(0,-1,![]() ),D(
),D(![]() ,-1,0),C(0,2,0),
,-1,0),C(0,2,0),
因而E(0,![]() ,
,![]() ), F(
), F(![]() ,
,![]() ,0),
,0),
由题得平面BFC的一个法向量为n1=(0,0,1).
设平面BEF的法向量为n2=(x,y,z),
又![]() =(
=(![]() ,
,![]() ,0),
,0),![]() =(0,
=(0,![]() ,
,![]() ),由
),由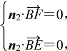
得其中一个n2=(1,-![]() ,1).
,1).
设二面角E-BF-C的大小为θ,且由题意知θ为锐角,
则cos θ=|cos〈n1,n2〉|=![]() =
=,
因此sin θ=![]() =
=![]() ,即二面角E-BF-C的正弦值为
,即二面角E-BF-C的正弦值为![]() .
.

【题目】二次函数图象上部分点的横坐标x,纵坐标y的对应值如下表:
x | … | -4 | -3 | -2 | -1 | 0 | 1 | … |
| … | 5 | 0 | -3 | -4 | -3 | m | … |
(1)m= ;
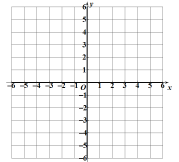
(2)在图中画出这个二次函数的图象;
(3)当![]() 时,x的取值范围是 ;
时,x的取值范围是 ;
(4)当![]() 时,y的取值范围是 .
时,y的取值范围是 .
【题目】某中学调查了某班全部![]() 名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
名同学参加书法社团和演讲社团的情况,数据如下表:(单位:人)
参加书法社团 | 未参加书法社团 | |
参加演讲社团 |
|
|
未参加演讲社团 |
|
|
(1)从该班随机选![]() 名同学,求该同学至少参加上述一个社团的概率;
名同学,求该同学至少参加上述一个社团的概率;
(2)在既参加书法社团又参加演讲社团的![]() 名同学中,有5名男同学
名同学中,有5名男同学![]()
![]() 名女同学
名女同学![]() 现从这
现从这![]() 名男同学和
名男同学和![]() 名女同学中各随机选
名女同学中各随机选![]() 人,求
人,求![]() 被选中且
被选中且![]() 未被选中的概率.
未被选中的概率.
【题目】某地区不同身高的未成年男性的体重平均值如下表.
身高/ | 60 | 70 | 80 | 90 | 100 | 110 | 120 | 130 | 140 | 150 | 160 | 170 |
体重/ | 6.13 | 7.90 | 9.99 | 12.15 | 15.02 | 17.50 | 20.92 | 26.86 | 31.11 | 38.85 | 47.25 | 55.05 |
(1)根据表格提供的数据,能否建立恰当的函数模型,使它能比较近似地反映这个地区未成年男性体重![]() 与身高
与身高![]() 的函数关系?试写出这个函数模型的关系式.
的函数关系?试写出这个函数模型的关系式.
(2)若体重超过相同身高男性体重平均值的1.2倍为偏胖,低于0.8倍为偏瘦,那么这个地区一名身高为![]() ,体重为
,体重为![]() 的在校男生的体重是否正常?
的在校男生的体重是否正常?