题目内容
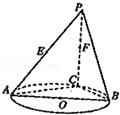
(2013•湖北)如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点.
(1)记平面BEF与平面ABC的交线为l,试判断直线l与平面PAC的位置关系,并加以证明;
(2)设(1)中的直线l与圆O的另一个交点为D,且点Q满足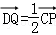 .记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
.记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
(1)记平面BEF与平面ABC的交线为l,试判断直线l与平面PAC的位置关系,并加以证明;
(2)设(1)中的直线l与圆O的另一个交点为D,且点Q满足
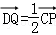 .记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
.记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
(1)l∥平面PAC,见解析 (2)见解析
(1)直线l∥平面PAC,证明如下:
连接EF,因为E,F分别是PA,PC的中点,所以EF∥AC,
又EF?平面ABC,且AC?平面ABC,所以EF∥平面ABC.
而EF?平面BEF,且平面BEF∩平面ABC=l,所以EF∥l.
因为l?平面PAC,EF?平面PAC,所以直线l∥平面PAC.
(2)(综合法)如图1,连接BD,由(1)可知交线l即为直线BD,且l∥AC.
因为AB是⊙O的直径,所以AC⊥BC,于是l⊥BC.
已知PC⊥平面ABC,而l?平面ABC,所以PC⊥l.
而PC∩BC=C,所以l⊥平面PBC.
连接BE,BF,因为BF?平面PBC,所以l⊥BF.
故∠CBF就是二面角E﹣l﹣C的平面角,即∠CBF=β.
由 ,作DQ∥CP,且
,作DQ∥CP,且 .
.
连接PQ,DF,因为F是CP的中点,CP=2PF,所以DQ=PF,
从而四边形DQPF是平行四边形,PQ∥FD.
连接CD,因为PC⊥平面ABC,所以CD是FD在平面ABC内的射影,
故∠CDF就是直线PQ与平面ABC所成的角,即∠CDF=θ.
又BD⊥平面PBC,有BD⊥BF,知∠BDF=α,
于是在Rt△DCF,Rt△FBD,Rt△BCF中,分别可得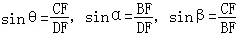 ,
,
从而 .
.
(2)(向量法)如图2,由 ,作DQ∥CP,且
,作DQ∥CP,且 .
.
连接PQ,EF,BE,BF,BD,由(1)可知交线l即为直线BD.
以点C为原点,向量 所在直线分别为x,y,z轴,建立如图所示的空间直角坐标系,
所在直线分别为x,y,z轴,建立如图所示的空间直角坐标系,
设CA=a,CB=b,CP=2c,则有
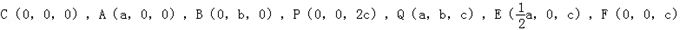 .
.
于是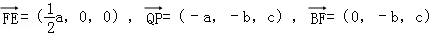 ,
,
∴ =
=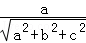 ,从而
,从而 ,
,
又取平面ABC的一个法向量为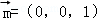 ,可得
,可得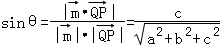 ,
,
设平面BEF的一个法向量为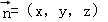 ,
,
所以由 可得
可得 .
.
于是 ,从而
,从而 .
.
故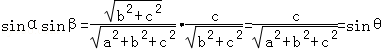 ,即sinθ=sinαsinβ.
,即sinθ=sinαsinβ.

连接EF,因为E,F分别是PA,PC的中点,所以EF∥AC,
又EF?平面ABC,且AC?平面ABC,所以EF∥平面ABC.
而EF?平面BEF,且平面BEF∩平面ABC=l,所以EF∥l.
因为l?平面PAC,EF?平面PAC,所以直线l∥平面PAC.
(2)(综合法)如图1,连接BD,由(1)可知交线l即为直线BD,且l∥AC.
因为AB是⊙O的直径,所以AC⊥BC,于是l⊥BC.
已知PC⊥平面ABC,而l?平面ABC,所以PC⊥l.
而PC∩BC=C,所以l⊥平面PBC.
连接BE,BF,因为BF?平面PBC,所以l⊥BF.
故∠CBF就是二面角E﹣l﹣C的平面角,即∠CBF=β.
由
 ,作DQ∥CP,且
,作DQ∥CP,且 .
.连接PQ,DF,因为F是CP的中点,CP=2PF,所以DQ=PF,
从而四边形DQPF是平行四边形,PQ∥FD.
连接CD,因为PC⊥平面ABC,所以CD是FD在平面ABC内的射影,
故∠CDF就是直线PQ与平面ABC所成的角,即∠CDF=θ.
又BD⊥平面PBC,有BD⊥BF,知∠BDF=α,
于是在Rt△DCF,Rt△FBD,Rt△BCF中,分别可得
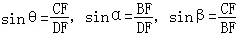 ,
,从而
 .
.(2)(向量法)如图2,由
 ,作DQ∥CP,且
,作DQ∥CP,且 .
.连接PQ,EF,BE,BF,BD,由(1)可知交线l即为直线BD.
以点C为原点,向量
 所在直线分别为x,y,z轴,建立如图所示的空间直角坐标系,
所在直线分别为x,y,z轴,建立如图所示的空间直角坐标系,设CA=a,CB=b,CP=2c,则有
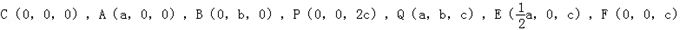 .
.于是
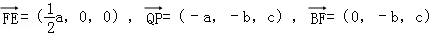 ,
,∴
 =
=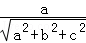 ,从而
,从而 ,
,又取平面ABC的一个法向量为
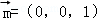 ,可得
,可得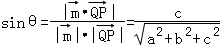 ,
,设平面BEF的一个法向量为
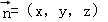 ,
,所以由
 可得
可得 .
.于是
 ,从而
,从而 .
.故
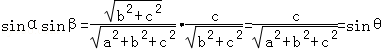 ,即sinθ=sinαsinβ.
,即sinθ=sinαsinβ.

练习册系列答案
相关题目
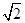 ,CD⊥AB,垂足为D.
,CD⊥AB,垂足为D.
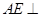 平面
平面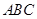 ,
,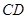 ∥
∥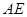 ,
,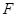 是
是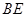 的中点,
的中点,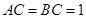 ,
,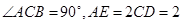 .
.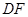 ∥平面
∥平面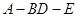 的大小的余弦值.
的大小的余弦值.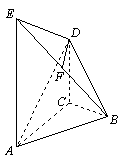
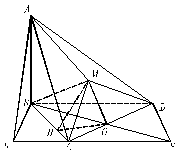
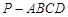 中,
中, 平面
平面 ,
, ,且
,且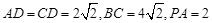 ,点
,点 在
在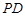 上.
上.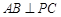 ;
;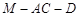 的大小为
的大小为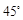 ,求
,求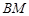 与平面
与平面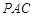 所成角的正弦值.
所成角的正弦值.
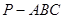 中,直线
中,直线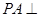 平面
平面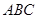 ,且
,且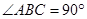 ,又点
,又点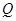 ,
,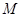 ,
,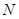 分别是线段
分别是线段 ,
,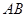 ,
,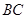 的中点,且点
的中点,且点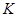 是线段
是线段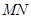 上的动点.
上的动点.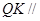 平面
平面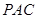 ;
;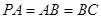 ,求二面角
,求二面角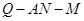 的平面角的余弦值.
的平面角的余弦值.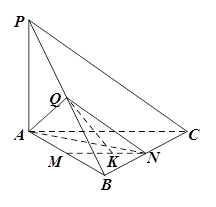
 ,点M,N分别在线段PA和BD上,BN=
,点M,N分别在线段PA和BD上,BN=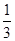 BD.
BD. ,求线段MN的长度.
,求线段MN的长度.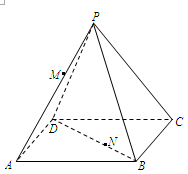
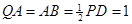 .
.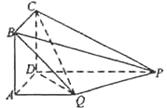
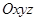 中,已知
中,已知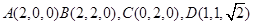 .若
.若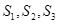 分别是三棱锥
分别是三棱锥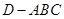 在
在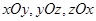 坐标平面上的正投影图形的面积,则( )
坐标平面上的正投影图形的面积,则( )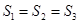
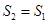 且
且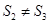
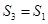 且
且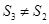
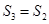 且
且