题目内容
如图,在正四棱锥P-ABCD中,PA=AB= ,点M,N分别在线段PA和BD上,BN=
,点M,N分别在线段PA和BD上,BN=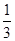 BD.
BD.
(1)若PM=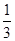 PA,求证:MN⊥AD;
PA,求证:MN⊥AD;
(2)若二面角M-BD-A的大小为 ,求线段MN的长度.
,求线段MN的长度.
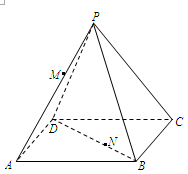
 ,点M,N分别在线段PA和BD上,BN=
,点M,N分别在线段PA和BD上,BN=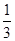 BD.
BD.(1)若PM=
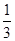 PA,求证:MN⊥AD;
PA,求证:MN⊥AD;(2)若二面角M-BD-A的大小为
 ,求线段MN的长度.
,求线段MN的长度.
(1)详见解析;(2)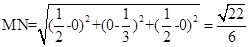 .
.
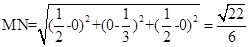 .
.试题分析:(1)由于这是一个正四棱锥,故易建立空间坐标系,易得各点的坐标,由
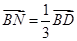 ,得
,得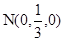 ,由
,由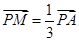 ,得
,得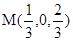 ,即可求得向量的坐标:
,即可求得向量的坐标: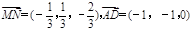 .不难计算出它们的数量积
.不难计算出它们的数量积 ,问题得证;(2)利用
,问题得证;(2)利用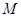 在
在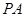 上,可设
上,可设 ,得出点的坐标
,得出点的坐标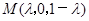 ,表示出
,表示出 ,进而求出平面
,进而求出平面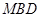 的法向量n=(λ-1,0,λ),由向量的夹角公式可得
的法向量n=(λ-1,0,λ),由向量的夹角公式可得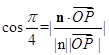 ,解得
,解得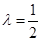 ,从而确定出
,从而确定出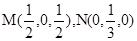 ,由两点间距离公式得
,由两点间距离公式得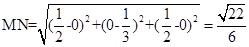 .
. 试题解析:证明:连接
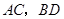 交于点
交于点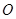 ,以
,以 为
为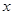 轴正方向,以
轴正方向,以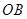 为
为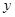 轴正方向,
轴正方向,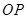 为
为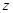 轴建立空间直角坐标系.
轴建立空间直角坐标系.因为
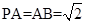 ,则
,则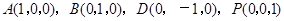 .
.(1)由
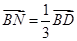 ,得
,得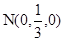 ,由
,由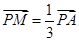 ,得
,得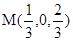 ,
,所以
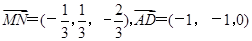 .
.因为
 .所以. 4分
.所以. 4分(2)因为
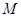 在
在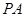 上,可设
上,可设 ,得
,得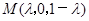 .
.所以
 .
.设平面
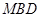 的法向量
的法向量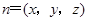 ,
,由
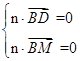 得
得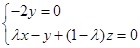
其中一组解为
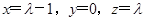 ,所以可取n=(λ-1,0,λ). 8分
,所以可取n=(λ-1,0,λ). 8分因为平面
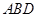 的法向量为
的法向量为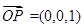 ,
,所以
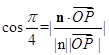 ,解得
,解得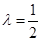 ,
, 从而
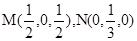 ,
,所以
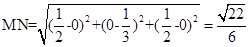 . 10分
. 10分
练习册系列答案
相关题目
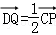 .记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
.记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.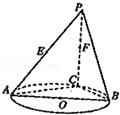
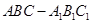 中,
中,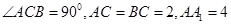 ,
, 是棱
是棱 的中点.如图所示.
的中点.如图所示.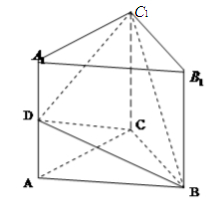
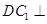 平面
平面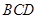 ;
;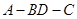 的大小.
的大小.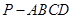 的底面为正方形,侧面
的底面为正方形,侧面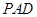
 底面
底面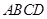 .
.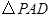 为等腰直角三角形,且
为等腰直角三角形,且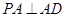 .
.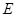 ,
,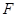 分别为底边
分别为底边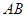 和侧棱
和侧棱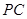 的中点.
的中点.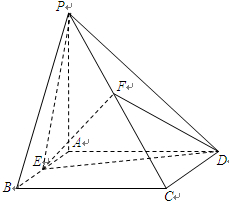
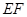 ∥平面
∥平面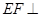 平面
平面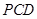 ;
; 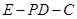 的余弦值.
的余弦值.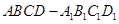 中,P是侧棱
中,P是侧棱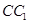 上的一点,
上的一点,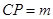 .
. 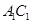 上是否存在一个定点
上是否存在一个定点 ,使得对任意的m,
,使得对任意的m,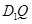 ⊥AP,并证明你的结论.
⊥AP,并证明你的结论. 
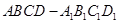 中
中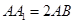 ,则
,则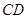 与平面
与平面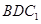 所成角的正弦值等于( )
所成角的正弦值等于( )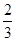
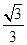
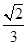
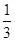
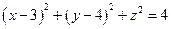 ,则
,则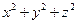 的最小值是( )
的最小值是( )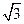
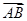 =(2,4,5),
=(2,4,5),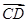 =(3,x,y),若
=(3,x,y),若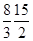
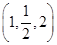 ,则m=________.
,则m=________.