题目内容
如图,在三棱锥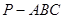 中,直线
中,直线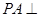 平面
平面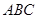 ,且
,且
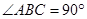 ,又点
,又点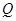 ,
,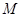 ,
,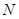 分别是线段
分别是线段 ,
,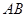 ,
,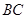 的中点,且点
的中点,且点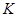 是线段
是线段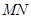 上的动点.
上的动点.
证明:直线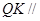 平面
平面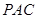 ;
;
(2) 若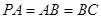 ,求二面角
,求二面角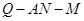 的平面角的余弦值.
的平面角的余弦值.
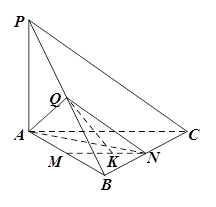
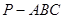 中,直线
中,直线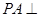 平面
平面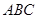 ,且
,且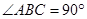 ,又点
,又点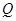 ,
,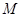 ,
,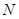 分别是线段
分别是线段 ,
,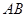 ,
,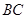 的中点,且点
的中点,且点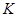 是线段
是线段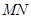 上的动点.
上的动点.证明:直线
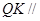 平面
平面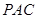 ;
;(2) 若
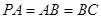 ,求二面角
,求二面角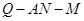 的平面角的余弦值.
的平面角的余弦值.
(1)参考解析;(2) 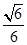
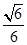
试题分析:(1)点
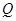 ,
,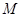 ,
,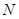 分别是线段
分别是线段 ,
,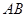 ,
,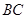 的中点所以
的中点所以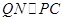 ,
, 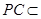 平面PAC.所以
平面PAC.所以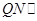 平面PAC.同理证明MN
平面PAC.同理证明MN 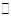 平面PAC.又由于
平面PAC.又由于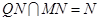 .所以平面QMN
.所以平面QMN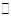 平面PAC.又
平面PAC.又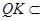 平面QMN.所以直线
平面QMN.所以直线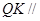 平面
平面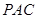 .
.(2)根据已知条件建立坐标系,写出关键点的坐标,并写出相应的向量,计算平面QAN与 MAN的法向量,求法向量的夹角,即可得到结论.
(1).连结QM 因为点
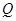 ,
,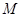 ,
,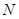 分别是线段
分别是线段 ,
,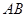 ,
,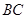 的中点
的中点所以QM∥PA MN∥AC QM∥平面PAC MN∥平面PAC
因为MN∩QM=M 所以平面QMN∥平面PAC QK
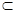 平面QMN
平面QMN所以QK∥平面PAC 7分
(2)方法1:过M作MH⊥AN于H,连QH,则∠QHM即为
二面角
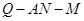 的平面角, 令
的平面角, 令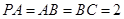
即QM=AM=1所以
此时sin∠MAH=sin∠BAN=
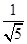 MH=
MH=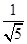 记二面角
记二面角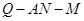 的平面角为
的平面角为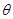
则tan
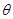 =
=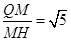 COS
COS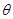 =
=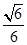 即为所求。 14分
即为所求。 14分方法2:以B为原点,以BC、BA所在直线为x轴y轴建空间直角坐标系,设
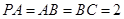
则A(0,2,0),M(0,1,0),N(1,0,0),p(0,2,2),Q(0,1,1),
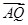 ="(0,-1,1),"
="(0,-1,1)," 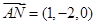
记
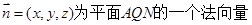 ,则
,则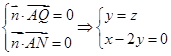
取
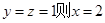
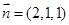
又平面ANM的一个法向量
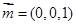 ,所以cos
,所以cos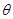 =
=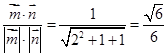
即为所求。 14分

练习册系列答案
相关题目
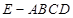 中,平面
中,平面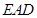
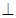 平面
平面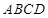 ,
,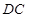 //
//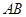 ,
,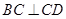 ,
,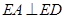 ,且
,且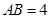 ,
,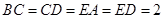 .
.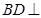 平面
平面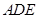 ;
;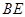 和平面
和平面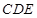 所成角的正弦值;
所成角的正弦值; 上是否存在一点
上是否存在一点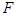 使得平面
使得平面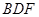
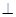 平面
平面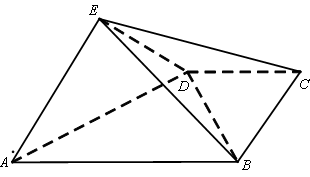
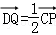 .记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
.记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.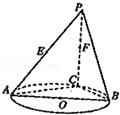
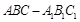 中,
中,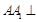 底面
底面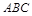 ,
,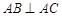 ,
,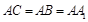 ,
,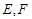 分别是棱
分别是棱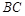 ,
,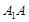 的中点,
的中点,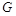 为棱
为棱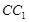 上的一点,且
上的一点,且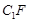 //平面
//平面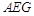 .
.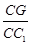 的值;
的值;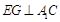 ;
;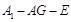 的余弦值.
的余弦值.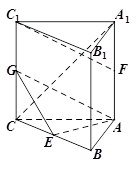
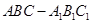 中,
中,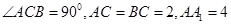 ,
,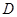 是棱
是棱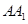 的中点.如图所示.
的中点.如图所示.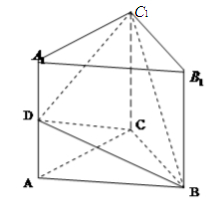
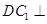 平面
平面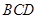 ;
; 的大小.
的大小.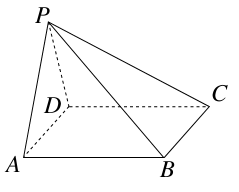
 中,P是侧棱
中,P是侧棱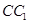 上的一点,
上的一点,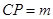 .
. 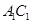 上是否存在一个定点
上是否存在一个定点 ,使得对任意的m,
,使得对任意的m,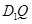 ⊥AP,并证明你的结论.
⊥AP,并证明你的结论. 
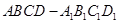 中
中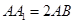 ,则
,则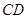 与平面
与平面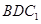 所成角的正弦值等于( )
所成角的正弦值等于( )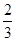
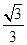
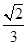
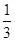
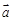 =(2, –2, 1), 已知P(-1, 3, 2),则P到平面OAB的距离等于 ( )
=(2, –2, 1), 已知P(-1, 3, 2),则P到平面OAB的距离等于 ( )