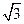题目内容
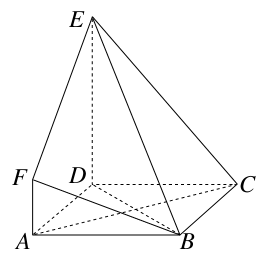
如图,在四棱锥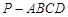 中,
中, 平面
平面 ,
, ,且
,且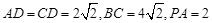 ,点
,点 在
在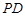 上.
上.
(1)求证: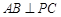 ;
;
(2)若二面角 的大小为
的大小为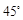 ,求
,求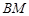 与平面
与平面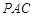 所成角的正弦值.
所成角的正弦值.

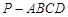 中,
中, 平面
平面 ,
, ,且
,且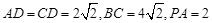 ,点
,点 在
在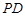 上.
上.(1)求证:
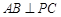 ;
;(2)若二面角
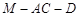 的大小为
的大小为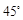 ,求
,求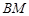 与平面
与平面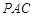 所成角的正弦值.
所成角的正弦值.
(1)详见解析;(2)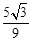
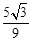
试题分析:(1)要证明直线和直线垂直,往往利用直线和平面垂直的性质,先证明线面垂直,进而证明直线和直线垂直.本题可先证明
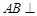 平面
平面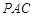 ,因
,因 平面
平面 ,所以
,所以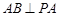 ,故只需证明
,故只需证明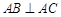 ,可放在
,可放在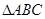 中利用平面几何的知识证明;(2)以以
中利用平面几何的知识证明;(2)以以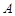 为原点,分别以射线
为原点,分别以射线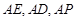 为
为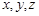 轴的正半轴,建立空间直角坐标系
轴的正半轴,建立空间直角坐标系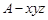 .分别表示相关点的坐标,通过二面角
.分别表示相关点的坐标,通过二面角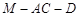 的大小为
的大小为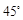 ,确定点
,确定点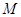 的坐标,再求直线
的坐标,再求直线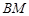 的方向向量
的方向向量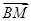 和面
和面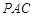 的法向量的夹角余弦,其绝对值即所求
的法向量的夹角余弦,其绝对值即所求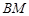 与平面
与平面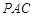 所成角的正弦值.
所成角的正弦值.(1)如图,设
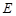 为
为 的中点,连结
的中点,连结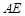 ,
,则
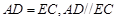 ,所以四边形
,所以四边形 为平行四边形,
为平行四边形,故
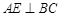 ,又
,又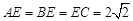 ,
,所以
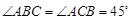 ,故
,故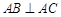 ,
,又因为
 平面
平面 ,所以
,所以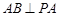 ,
,且
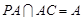 ,所以
,所以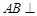 平面
平面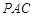 ,故有
,故有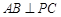 5分
5分
(2)如图,以
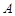 为原点,分别以射线
为原点,分别以射线
为
 轴的正半轴,建立空间直角坐标系
轴的正半轴,建立空间直角坐标系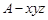 .
.则
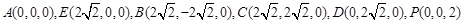 ,
,设
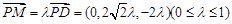 ,易得
,易得 ,
,设平面
 的一个法向量为
的一个法向量为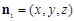 ,则
,则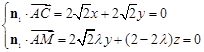 ,
,令
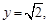 得
得 ,即
,即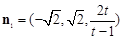 .
.又平面
 的一个法向量为
的一个法向量为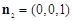 ,
,由题知
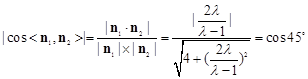 ,解得
,解得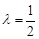 ,
,即
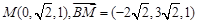 ,而
,而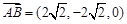 是平面
是平面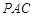 的一个法向量,
的一个法向量,设平面
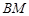 与平面
与平面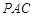 所成的角为
所成的角为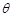 ,则
,则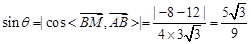 .
.故直线
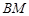 与平面
与平面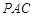 所成的角的正弦值为
所成的角的正弦值为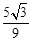 . 12分
. 12分
练习册系列答案
相关题目
 中,
中,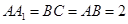 ,
,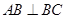 。M、N分别是AC和BB1的中点。
。M、N分别是AC和BB1的中点。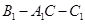 的大小。
的大小。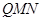 ⊥平面
⊥平面 ,
, 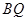 的长度。
的长度。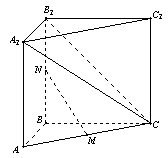
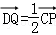 .记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.
.记直线PQ与平面ABC所成的角为θ,异面直线PQ与EF所成的角为α,二面角E﹣l﹣C的大小为β.求证:sinθ=sinαsinβ.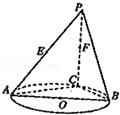
 中,
中,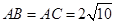 ,
, ,
,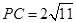 ,点
,点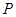 在平面
在平面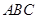 内的射影恰为
内的射影恰为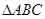 的重心
的重心 ,M为侧棱
,M为侧棱 上一动点.
上一动点.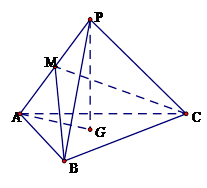
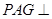 平面
平面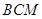 ;
;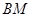 与平面
与平面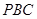 所成角的正弦值.
所成角的正弦值.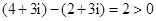 ,所以
,所以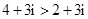 ;
;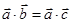 两边同除
两边同除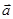 ,可得
,可得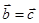 ;
; 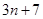 的一个通项公式是
的一个通项公式是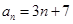 ;
;  中,P是侧棱
中,P是侧棱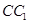 上的一点,
上的一点,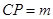 .
. 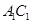 上是否存在一个定点
上是否存在一个定点 ,使得对任意的m,
,使得对任意的m,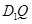 ⊥AP,并证明你的结论.
⊥AP,并证明你的结论. 
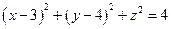 ,则
,则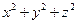 的最小值是( )
的最小值是( )