题目内容
2.已知函数y=f(x)的导函数为f′(x),且$f(x)={x^2}f'(\frac{π}{3})+sinx$,则$f'(\frac{π}{3})$=( )| A. | $\frac{3}{6-4π}$ | B. | $\frac{3}{6-2π}$ | C. | $\frac{3}{6+4π}$ | D. | $\frac{3}{6+2π}$ |
分析 先根据导数的运算法则求导,再代入值计算即可.
解答 解:∵$f(x)={x^2}f'(\frac{π}{3})+sinx$,
∴f′(x)=2f′($\frac{π}{3}$)x+cosx,
∴f′($\frac{π}{3}$)=2f′($\frac{π}{3}$)×$\frac{π}{3}$+cos$\frac{π}{3}$,
解得f′($\frac{π}{3}$)=$\frac{3}{6-4π}$,
故选:A
点评 本题考查了导数的运算法则和导数值的求法,属于基础题.

练习册系列答案
相关题目
3.已知a,b∈R,则“a2+b2≤1”是“|a|+|b|≤1”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
4.已知i为虚数单位,复数z=a+bi(a,b∈R),则“z2≥0”是“b=0”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分又不必要条件 |
17.已知直线x+y=1与圆x2+y2=1 相交A,B两点,则|AB|=( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
14.设等差数列{an}的前n项和为Sn,若a1>0,3a8=5a13,则Sn中最大的是( )
| A. | S10 | B. | S11 | C. | S20 | D. | S21 |
11.已知i是虚数单位,若-2iz=1-i,则z所表示的复平面上的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
12.阅读右边的程序框图,运行相应的程序,则输出s,k的值依次为( )
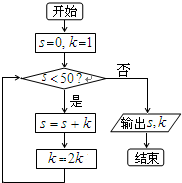

| A. | 32,63 | B. | 64,63 | C. | 63,32 | D. | 63,64 |




