题目内容
5. 四边形OABC的四个顶点坐标分别为O(0,0),A(6,2),B(4,6),C(2,6),直线y=kx($\frac{1}{3}$<k<3)把四边形OABC分成两部分,S表示靠近x轴一侧那部分的面积.
四边形OABC的四个顶点坐标分别为O(0,0),A(6,2),B(4,6),C(2,6),直线y=kx($\frac{1}{3}$<k<3)把四边形OABC分成两部分,S表示靠近x轴一侧那部分的面积.(1)求S=f(k)的函数表达式;
(2)当k为何值时,直线y=kx将四边形OABC分为面积相等的两部分.
分析 (1)由题意画出图象,求出|OA|、|BC|、直线OA的方程,由点到直线的距离求出点B到直线OA的距离,求出四边形OABC的面积S,根据图象分类讨论,分别由图象求出靠近x轴一侧那部分的面积表达式,再用分段函数的形式表示出来;
(2)由(1)和条件列出方程求出k的值.
解答 解:(1)由题意画出图象: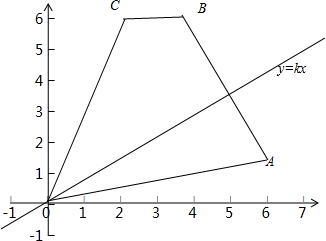 |OA|=$\sqrt{36+4}$=2$\sqrt{10}$,|BC|=2,
|OA|=$\sqrt{36+4}$=2$\sqrt{10}$,|BC|=2,
直线OA的方程是y=$\frac{1}{3}$x,则x-3y=0,
∴点B到直线OA的距离d=$\frac{|4-18|}{\sqrt{1+9}}$=$\frac{14}{\sqrt{10}}$,
则四边形OABC的面积S=S△AOB+S△BOC=$\frac{1}{2}×2\sqrt{10}×\frac{14}{\sqrt{10}}+\frac{1}{2}×2×6$=20,
①当直线y=kx与AB相交时,此时$\frac{1}{3}<k≤\frac{3}{2}$,
由A(6,2),B(4,6),得直线AB的方程是y-2=$\frac{6-2}{4-6}$(x-6),即y=-2x+14,
由$\left\{\begin{array}{l}{y=kx}\\{y=-2x+14}\end{array}\right.$得,x=$\frac{14}{k+2}$,y=$\frac{14k}{k+2}$,
∴直线AB与直线y=kx的交点坐标是P($\frac{14}{k+2}$,$\frac{14k}{k+2}$),
则点P到直线OA的距离d′=$\frac{|\frac{14}{k+2}-3×\frac{14k}{k+2}|}{\sqrt{1+9}}$=$\frac{14|}{\sqrt{10}}|\frac{1-3k}{k+2}|$,
∴△POA的面积S=$\frac{1}{2}×|OA|×d′$=$\frac{1}{2}×2\sqrt{10}×\frac{14|}{\sqrt{10}}|\frac{1-3k}{k+2}|$=$14|\frac{1-3k}{k+2}|$;
②当直线y=kx与BC相交时,此时$\frac{3}{2}<k<3$,
则交点坐标是($\frac{6}{k}$,6),
∴靠近x轴一侧那部分的面积S=20-$\frac{1}{2}×6×(\frac{6}{k}-2)$=$26-\frac{18}{k}$,
∴S=f(k)=$\left\{\begin{array}{l}{14|\frac{1-3k}{k+2}|,\frac{1}{3}<k≤\frac{3}{2}}\\{26-\frac{18}{k},\frac{3}{2}<k<3}\end{array}\right.$;
(2)由(1)可知,当直线y=kx与AB相交时,此时$\frac{1}{3}<k≤\frac{3}{2}$,
直线y=kx可将四边形OABC分为面积相等的两部分,
∴$14|\frac{1-3k}{k+2}|$=$\frac{1}{2}×20$,解得k=$\frac{-3}{26}$或$\frac{17}{16}$,
则k的值是$\frac{17}{16}$.
点评 本题考查分段函数在实际生活中的应用,两点之间、点到直线的距离公式,直线方程的求法等等,以及分割法求图形的面积,考查分类讨论思想,数形结合思想,化简、计算能力,属于中档题.

| A. | 5$\sqrt{5}$ | B. | 4$\sqrt{5}$ | C. | 3$\sqrt{5}$ | D. | $2\sqrt{5}$ |
| A. | (-∞,1] | B. | [0,1] | C. | (-2,-1)∪(-1,1] | D. | (-∞,-2)∪(-1,1] |
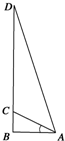
 如图所示,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=30°以及∠MAC=105°;从C点测得∠MCA=45°.已知山高BC=150米,则所求山高MN为( )米.
如图所示,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=30°以及∠MAC=105°;从C点测得∠MCA=45°.已知山高BC=150米,则所求山高MN为( )米.| A. | 300$\sqrt{3}$ | B. | 150$\sqrt{6}$ | C. | 150$\sqrt{3}$ | D. | 300$\sqrt{6}$ |
| A. | [2,+∞) | B. | (2,+∞) | C. | (-∞,2] | D. | (-∞,2) |
| A. | 5$\sqrt{2}$ | B. | 10$\sqrt{2}$ | C. | 15$\sqrt{2}$ | D. | 20$\sqrt{2}$ |
