题目内容
15.在△ABC中,角A,B,C的对边分别为a,b,c,已知$\frac{b}{c}$=$\frac{2\sqrt{3}}{3}$,A+3C=B,(1)求cosC的值;
(2)若b=3$\sqrt{3}$,求△ABC的面积.
分析 (1)把A+3C=B代入A+B+C=π得B=$\frac{π}{2}$+C,可得sinB=cosC>0,由条件和正弦定理化简后,利用平方关系求出cosC的值;
(2)由条件求出边c的值,由(1)和平方关系求出cosB和sinC的值,利用两角和的正弦公式求出sinA的值,代入三角形的面积公式求解即可.
解答 解:(1)由题意得A+3C=B,则A=B-3C,
代入A+B+C=π得,B=$\frac{π}{2}$+C,所以sinB=cosC>0,
∵$\frac{b}{c}=\frac{2\sqrt{3}}{3}$,∴由正弦定理得,$\frac{sinB}{sinC}=\frac{2\sqrt{3}}{3}$,则$\frac{cosC}{sinC}=\frac{2\sqrt{3}}{3}$,①
又sin2C+cos2C=1,②
由①②得,cos2C=$\frac{4}{7}$,则cosC=$\frac{2\sqrt{7}}{7}$;
(2)∵$\frac{b}{c}=\frac{2\sqrt{3}}{3}$,b=3$\sqrt{3}$,∴c=$\frac{9}{2}$,
由(1)知sinB=cosC=$\frac{2\sqrt{7}}{7}$,且B=$\frac{π}{2}$+C,
∴cosB=-$\sqrt{1-si{n}^{2}B}$=-$\frac{\sqrt{21}}{7}$,同理可得sinC=$\frac{\sqrt{21}}{7}$,
则sinA=sin(B+C)=sinBcosC+cosBsinC
=$\frac{2\sqrt{7}}{7}$×$\frac{2\sqrt{7}}{7}$+(-$\frac{\sqrt{21}}{7}$)×$\frac{\sqrt{21}}{7}$=$\frac{1}{7}$
∴△ABC的面积S=$\frac{1}{2}bcsinA$=$\frac{1}{2}×3\sqrt{3}×\frac{9}{2}×\frac{1}{7}$=$\frac{27\sqrt{3}}{28}$.
点评 本题考查正弦定理,平方关系,两角和的正弦公式,以及三角形的面积公式的应用,注意内角的范围,属于中档题.

| A. | a1=3,q=2 | B. | a1=-3,q=2 | C. | a1=3,q=-2 | D. | a1=-3,q=-2 |
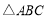 的一个内角为
的一个内角为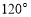 ,并且三边长构成公差为4的等差数列,则
,并且三边长构成公差为4的等差数列,则 四边形OABC的四个顶点坐标分别为O(0,0),A(6,2),B(4,6),C(2,6),直线y=kx($\frac{1}{3}$<k<3)把四边形OABC分成两部分,S表示靠近x轴一侧那部分的面积.
四边形OABC的四个顶点坐标分别为O(0,0),A(6,2),B(4,6),C(2,6),直线y=kx($\frac{1}{3}$<k<3)把四边形OABC分成两部分,S表示靠近x轴一侧那部分的面积.