题目内容
16.直线x+2y+1=0被圆(x-2)2+(y-1)2=25所截得的弦长为( )| A. | 5$\sqrt{5}$ | B. | 4$\sqrt{5}$ | C. | 3$\sqrt{5}$ | D. | $2\sqrt{5}$ |
分析 易得圆的圆心和半径r,可得圆心到直线x+2y-10=0的距离d,代入弦长公式2$\sqrt{{r}^{2}-{d}^{2}}$,计算可得答案.
解答 解:由题意可得圆(x-2)2+(y-1)2=25的圆心为(2,1),半径r=5,
故圆心到直线x+2y+1=0的距离d=$\frac{|2+2+1|}{\sqrt{{1}^{2}+{2}^{2}}}$=$\sqrt{5}$,
故所求的弦长为2$\sqrt{{r}^{2}-{d}^{2}}$=4$\sqrt{5}$,
故选:B
点评 本题考查直线与圆的位置关系,涉及圆的弦长的求解,属中档题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
4.已知等比数列的前n项和公式Sn=3(1-2n),则其首项a1和公比q分别为( )
| A. | a1=3,q=2 | B. | a1=-3,q=2 | C. | a1=3,q=-2 | D. | a1=-3,q=-2 |
 四边形OABC的四个顶点坐标分别为O(0,0),A(6,2),B(4,6),C(2,6),直线y=kx($\frac{1}{3}$<k<3)把四边形OABC分成两部分,S表示靠近x轴一侧那部分的面积.
四边形OABC的四个顶点坐标分别为O(0,0),A(6,2),B(4,6),C(2,6),直线y=kx($\frac{1}{3}$<k<3)把四边形OABC分成两部分,S表示靠近x轴一侧那部分的面积.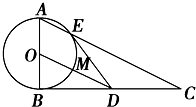 如图,△ABC是直角三角形,∠ABC=90°,以AB为直径的圆O交AC于点E,过E作圆的切线交BC于D点.连结OD交圆O于点M.
如图,△ABC是直角三角形,∠ABC=90°,以AB为直径的圆O交AC于点E,过E作圆的切线交BC于D点.连结OD交圆O于点M.