题目内容
14.△ABC的内角A、B、C所对的边为a、b、c,则下列命题正确的是②③.①若A<B,则 cos2A<cos2B ②若ab>c2,则C$<\frac{π}{3}$
③若a+b>2c,则 C$<\frac{π}{3}$ ④若(a+b)c<2ab,则C>$\frac{π}{2}$.
分析 ①和④取满足条件,不满足结论,判断为错误;②利用余弦定理,将c2放大为ab,再结合均值定理即可证明cosC>$\frac{1}{2}$,从而证明C<$\frac{π}{3}$;③利用余弦定理,将c2放大为($\frac{a+b}{2}$)2,再结合均值定理即可证明cosC>$\frac{1}{2}$,从而证明C<$\frac{π}{3}$.
解答 解:①取A=30°,B=45°,满足A<B,此时cos2A=cos60°=$\frac{1}{2}$,cos2B=cos90°=0,得到cos2A>cos2B,故①错误;
②ab>c2⇒cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$>$\frac{2ab-ab}{2ab}$=$\frac{1}{2}$⇒C<$\frac{π}{3}$,故②正确;
③a+b>2c⇒cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$>$\frac{4({a}^{2}+{b}^{2})-(a+b)^{2}}{8ab}$≥$\frac{3}{8}$×$\frac{{a}^{2}+{b}^{2}}{ab}$-$\frac{1}{4}$≥$\frac{2}{4}$=$\frac{1}{2}$⇒C<$\frac{π}{3}$,故③正确;
④取a=b=2,c=1,满足(a+b)c<2ab得:C<$\frac{π}{3}$<$\frac{π}{2}$,故④错误;
故答案为:②③
点评 此题考查了余弦定理,放缩法证明不等式的技巧,反证法和举反例法证明不等式,熟练掌握运算法则是解本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
4.已知等比数列的前n项和公式Sn=3(1-2n),则其首项a1和公比q分别为( )
| A. | a1=3,q=2 | B. | a1=-3,q=2 | C. | a1=3,q=-2 | D. | a1=-3,q=-2 |
3.下列说法正确的是( )
| A. | 某人打靶,射击10次,击中7次,那么此人中靶的概率为0.7 | |
| B. | 一位同学做掷硬币试验,掷6次,一定有3次“正面朝上” | |
| C. | 某地发行福利彩票,回报率为47%,有人花了100元钱买彩票,一定会有47元的回报 | |
| D. | 概率等于1的事件不一定为必然事件 |
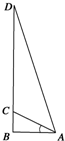 四边形OABC的四个顶点坐标分别为O(0,0),A(6,2),B(4,6),C(2,6),直线y=kx($\frac{1}{3}$<k<3)把四边形OABC分成两部分,S表示靠近x轴一侧那部分的面积.
四边形OABC的四个顶点坐标分别为O(0,0),A(6,2),B(4,6),C(2,6),直线y=kx($\frac{1}{3}$<k<3)把四边形OABC分成两部分,S表示靠近x轴一侧那部分的面积.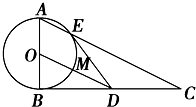 如图,△ABC是直角三角形,∠ABC=90°,以AB为直径的圆O交AC于点E,过E作圆的切线交BC于D点.连结OD交圆O于点M.
如图,△ABC是直角三角形,∠ABC=90°,以AB为直径的圆O交AC于点E,过E作圆的切线交BC于D点.连结OD交圆O于点M.