Question

9．正方体ABCD-A₁B₁C₁D₁的棱长为a，$\overrightarrow{AM}=\frac{1}{3}\overrightarrow{A{C_1}}$，N是BB₁的中点，则|MN|=（　　）

• A． $\frac{{\sqrt{21}}}{6}a$
• B． $\frac{{\sqrt{6}}}{6}a$
• C． $\frac{{\sqrt{15}}}{6}a$
• D． $\frac{{\sqrt{15}}}{3}a$

Answer 1

分析 把向量$\overrightarrow{MN}$用基底＜$\overrightarrow{AB}，\overrightarrow{AD}，\overrightarrow{A{A}_{1}}$＞表示，然后利用向量的数量积运算得答案．

解答 解：如图，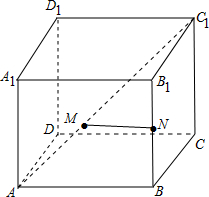

$\overrightarrow{MN}=\overrightarrow{AN}-\overrightarrow{AM}$=$\overrightarrow{AB}+\overrightarrow{BN}$-$\frac{1}{3}\overrightarrow{A{C}_{1}}$=$\overrightarrow{AB}$$+\frac{1}{2}\overrightarrow{A{A}_{1}}$$-\frac{1}{3}\overrightarrow{AB}-\frac{1}{3}\overrightarrow{AD}-\frac{1}{3}\overrightarrow{A{A}_{1}}$
=$\frac{2}{3}\overrightarrow{AB}-\frac{1}{3}\overrightarrow{AD}-\frac{1}{6}\overrightarrow{A{A}_{1}}$．
∴$|\overrightarrow{MN}{|}^{2}=（\frac{2}{3}\overrightarrow{AB}-\frac{1}{3}\overrightarrow{AD}-\frac{1}{6}\overrightarrow{A{A}_{1}}）^{2}$=$（\frac{2}{3}|\overrightarrow{AB}|）^{2}+（\frac{1}{3}|\overrightarrow{AD}|）^{2}+（\frac{1}{6}|\overrightarrow{A{A}_{1}}|）^{2}$=$\frac{21}{36}{a}^{2}$．
∴$|MN|=\frac{\sqrt{21}}{6}a$．
故选：A．

点评 本题考查了棱柱的结构特征，考查了平面向量的数量积运算，考查了向量模的求法，是基础题．