题目内容
18. 如图,正方体ABCD-A1B1C1D1的棱长为2,M,N分别是C1D1,CC1的中点,则直线B1N与平面BDM所成角的正弦值为$\frac{{\sqrt{5}}}{3}$.
如图,正方体ABCD-A1B1C1D1的棱长为2,M,N分别是C1D1,CC1的中点,则直线B1N与平面BDM所成角的正弦值为$\frac{{\sqrt{5}}}{3}$.
分析 建立如图所示的坐标系,求出平面BDM的法向量,利用向量的夹角公式求出直线B1N与平面BDM所成角的正弦值.
解答  解:建立如图所示的坐标系,则B1(2,2,2),N(0,2,1),B(2,2,0),D(0,0,0),M(0,1,2).
解:建立如图所示的坐标系,则B1(2,2,2),N(0,2,1),B(2,2,0),D(0,0,0),M(0,1,2).
设平面BDM的法向量为$\overrightarrow{n}$=(x,y,z),则
∵$\overrightarrow{DB}$=(2,2,0),$\overrightarrow{DM}$=(0,1,2),
∴$\left\{\begin{array}{l}{2x+2y=0}\\{y+2z=0}\end{array}\right.$,
∴$\overrightarrow{n}$=(2,-2,1),
∵$\overrightarrow{{B}_{1}N}$=(-2,0,-1),
∴直线B1N与平面BDM所成角的正弦值为|$\frac{-4-1}{\sqrt{4+4+1}•\sqrt{4+1}}$|=$\frac{{\sqrt{5}}}{3}$.
故答案为:$\frac{{\sqrt{5}}}{3}$.
点评 本题考查直线B1N与平面BDM所成角的正弦值,考查向量法的运用,正确求出平面BDM的法向量是关键.

练习册系列答案
相关题目
9.正方体ABCD-A1B1C1D1的棱长为a,$\overrightarrow{AM}=\frac{1}{3}\overrightarrow{A{C_1}}$,N是BB1的中点,则|MN|=( )
| A. | $\frac{{\sqrt{21}}}{6}a$ | B. | $\frac{{\sqrt{6}}}{6}a$ | C. | $\frac{{\sqrt{15}}}{6}a$ | D. | $\frac{{\sqrt{15}}}{3}a$ |
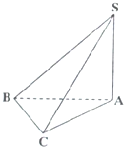 如图,在三棱锥S-ABC中,SA⊥底面ABC,AC⊥BC,若AC=BC=1,SA=AB,则SB与平面SAC所成角的大小为30°.
如图,在三棱锥S-ABC中,SA⊥底面ABC,AC⊥BC,若AC=BC=1,SA=AB,则SB与平面SAC所成角的大小为30°. 如图,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.
如图,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.