题目内容
15.求值:$\frac{1+sinα}{\sqrt{1+cosα}-\sqrt{1-cosα}}$+$\frac{1-sinα}{\sqrt{1+cosα}+\sqrt{1-cosα}}$,其中$π<α<\frac{3π}{2}$.分析 直接利用二倍角的余弦函数结合角的范围,化简求解即可.
解答 解:∵$π<α<\frac{3π}{2}$,∴$\frac{π}{2}<\frac{α}{2}<\frac{3π}{4}$,
∴$\frac{1+sinα}{\sqrt{1+cosα}-\sqrt{1-cosα}}$+$\frac{1-sinα}{\sqrt{1+cosα}+\sqrt{1-cosα}}$=$\frac{1+sinα}{\sqrt{2{cos}^{2}\frac{α}{2}}-\sqrt{2{sin}^{2}\frac{α}{2}}}$$+\frac{1-sinα}{\sqrt{2{cos}^{2}\frac{α}{2}}+\sqrt{2{sin}^{2}\frac{α}{2}}}$
=$\frac{1+sinα}{-\sqrt{2}(cos\frac{α}{2}+sin\frac{α}{2})}$+$\frac{1-sinα}{\sqrt{2}(-cos\frac{α}{2}+sin\frac{α}{2})}$
=$\frac{cos\frac{α}{2}+sin\frac{α}{2}}{-\sqrt{2}}$+$\frac{-cos\frac{α}{2}+sin\frac{α}{2}}{\sqrt{2}}$
=-$\sqrt{2}$$cos\frac{π}{2}$.
点评 本题考查二倍角个数的应用,三角函数的化简求值,考查计算能力.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
6.从2,3,4,5,6,7,8,9这8个数中任取2个不同的数分别作为一个对数的底数和真数,则可以组成不同对数值的个数为( )
| A. | 56 | B. | 54 | C. | 53 | D. | 52 |
20.1+(1+x)+(1+x)2+…+(1+x)100的展开式的各项系数之和为( )
| A. | 199 | B. | 2100-1 | C. | 2101-1 | D. | 2100 |
9.正方体ABCD-A1B1C1D1的棱长为a,$\overrightarrow{AM}=\frac{1}{3}\overrightarrow{A{C_1}}$,N是BB1的中点,则|MN|=( )
| A. | $\frac{{\sqrt{21}}}{6}a$ | B. | $\frac{{\sqrt{6}}}{6}a$ | C. | $\frac{{\sqrt{15}}}{6}a$ | D. | $\frac{{\sqrt{15}}}{3}a$ |
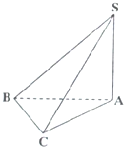 如图,在三棱锥S-ABC中,SA⊥底面ABC,AC⊥BC,若AC=BC=1,SA=AB,则SB与平面SAC所成角的大小为30°.
如图,在三棱锥S-ABC中,SA⊥底面ABC,AC⊥BC,若AC=BC=1,SA=AB,则SB与平面SAC所成角的大小为30°.