题目内容
19.经过点P(1,0),斜率为$\frac{3}{4}$的直线和抛物线y2=x交于A、B两点,若线段AB中的点为M,则M的坐标为($\frac{17}{9}$,$\frac{2}{3}$).分析 设A(x1,y1),B(x2,y2).由已知可得直线AB的方程为:y=3(x-2),与抛物线的方程联立可得根与系数的关系.利用弦长公式即可得出.
解答 解:设A(x1,y1),B(x2,y2).
由已知可得直线AB的方程为:y=$\frac{3}{4}$(x-1),
联立$\left\{\begin{array}{l}{y}^{2}=x\\ y=\frac{3}{4}(x-1)\end{array}\right.$化为9x2-34x+9=0,
∴x1+x2=$\frac{34}{9}$,x1x2=1.中点M的坐标($\frac{17}{9}$,$\frac{2}{3}$)
故答案为:($\frac{17}{9}$,$\frac{2}{3}$).
点评 本题考查了直线与抛物线的综合应用,弦长公式的应用,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
9.正方体ABCD-A1B1C1D1的棱长为a,$\overrightarrow{AM}=\frac{1}{3}\overrightarrow{A{C_1}}$,N是BB1的中点,则|MN|=( )
| A. | $\frac{{\sqrt{21}}}{6}a$ | B. | $\frac{{\sqrt{6}}}{6}a$ | C. | $\frac{{\sqrt{15}}}{6}a$ | D. | $\frac{{\sqrt{15}}}{3}a$ |
11.设集合A={1,lna},B={a,b},A∩B={2},则A∪B=( )
| A. | {1,2,e2} | B. | {1,2,$\frac{1}{{e}^{2}}$} | C. | {1,2,e,e2} | D. | {1,2,2e,e2} |
19.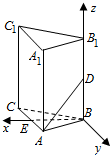 在正三棱柱ABC-A1B1C1中,已知AB=1,D在棱BB1上,且BD=1,则AD与平面ACC1A1所成的角的正弦值为( )
在正三棱柱ABC-A1B1C1中,已知AB=1,D在棱BB1上,且BD=1,则AD与平面ACC1A1所成的角的正弦值为( )
 在正三棱柱ABC-A1B1C1中,已知AB=1,D在棱BB1上,且BD=1,则AD与平面ACC1A1所成的角的正弦值为( )
在正三棱柱ABC-A1B1C1中,已知AB=1,D在棱BB1上,且BD=1,则AD与平面ACC1A1所成的角的正弦值为( )| A. | $\frac{{\sqrt{6}}}{4}$ | B. | -$\frac{{\sqrt{6}}}{4}$ | C. | $\frac{{\sqrt{10}}}{4}$ | D. | -$\frac{{\sqrt{10}}}{4}$ |
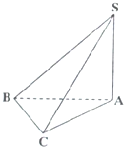 如图,在三棱锥S-ABC中,SA⊥底面ABC,AC⊥BC,若AC=BC=1,SA=AB,则SB与平面SAC所成角的大小为30°.
如图,在三棱锥S-ABC中,SA⊥底面ABC,AC⊥BC,若AC=BC=1,SA=AB,则SB与平面SAC所成角的大小为30°. 如图,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.
如图,PD⊥平面ABCD,AD⊥DC,AD∥BC,PD:DC:BC=1:1:$\sqrt{2}$.