题目内容
1.已知椭圆焦点在x轴上,短轴长为2,离心率为$\frac{\sqrt{3}}{2}$,直线l:y=-2任取椭圆上一点P(异于短轴端点M、N)直线MP、NP分别交直线l于点T、S,则|ST|的最小值为多少?分析 利用椭圆离心率的意义和a、b、c的关系即可求出椭圆的方程;先设出点T、S的坐标,可写出直线MT、NS的方程,联立即可得出点P的坐标,再代入椭圆方程即可得出s、t的关系,进而求出|ST|最小值.
解答  解:根据题意,得b=1,e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,
解:根据题意,得b=1,e=$\frac{c}{a}$=$\frac{\sqrt{3}}{2}$,
∴b2=1,a2=4,
∴椭圆方程为:$\frac{{x}^{2}}{4}$+y2=1,
设点S(s,-2),T(t,-2)不妨设t>0,s<0.
则直线SN的方程为:y=-$\frac{1}{s}$x-1;
直线TM的方程为:y=-$\frac{3}{t}$x+1.
联立直线SN、TM方程$\left\{\begin{array}{l}{y=-\frac{1}{s}x-1}\\{y=-\frac{3}{t}x+1}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=\frac{2ts}{3s-t}}\\{y=-\frac{3s+t}{3s-t}}\end{array}\right.$,
即点P($\frac{2ts}{3s-t}$,-$\frac{3s+t}{3s-t}$).
代入椭圆的方程得$\frac{{s}^{2}{t}^{2}}{(3s-t)^{2}}$+$\frac{(3s+t)^{2}}{(3s-t)^{2}}$=1,化为st=-12.
∴|ST|=t-s=t+$\frac{12}{t}$≥2$\sqrt{t•\frac{12}{t}}$=4$\sqrt{3}$,
当且仅当t=2$\sqrt{3}$时取等号,
即|ST|的最小值为4$\sqrt{3}$.
点评 本题考查椭圆的简单性质,熟练掌握椭圆的定义与性质、直线相交问题的解法是解决本题的关键,注意解题方法的积累,属于中档题.

 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案| A. | 56 | B. | 54 | C. | 53 | D. | 52 |
| A. | $\frac{{\sqrt{21}}}{6}a$ | B. | $\frac{{\sqrt{6}}}{6}a$ | C. | $\frac{{\sqrt{15}}}{6}a$ | D. | $\frac{{\sqrt{15}}}{3}a$ |
| A. | {1,2,e2} | B. | {1,2,$\frac{1}{{e}^{2}}$} | C. | {1,2,e,e2} | D. | {1,2,2e,e2} |
 已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA=1,PA⊥平面ABCD,E、F分别是线段AB、BC的中点.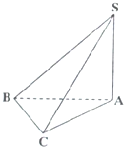 如图,在三棱锥S-ABC中,SA⊥底面ABC,AC⊥BC,若AC=BC=1,SA=AB,则SB与平面SAC所成角的大小为30°.
如图,在三棱锥S-ABC中,SA⊥底面ABC,AC⊥BC,若AC=BC=1,SA=AB,则SB与平面SAC所成角的大小为30°.