题目内容
12.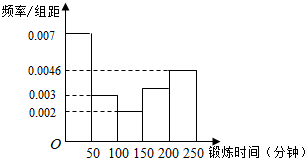 某个公司调查统计它的员工每周参与体育锻炼的时间,样本容量为100人,将调查结果统计为频率分布直方图,如图.我们将每周体育锻炼时间不低于150分钟的人称为“勤于锻炼者”,并将有关性别的信息统计到表中.
某个公司调查统计它的员工每周参与体育锻炼的时间,样本容量为100人,将调查结果统计为频率分布直方图,如图.我们将每周体育锻炼时间不低于150分钟的人称为“勤于锻炼者”,并将有关性别的信息统计到表中.| “勤于锻炼者” | 非“勤于锻炼者” | 合计 | |
| 男 | 25 | 70 | |
| 女 | |||
| 合计 |
附:X2=$\frac{n({n}_{11}{n}_{22}-{n}_{12}{n}_{21})^{2}}{{n}_{1}+{n}_{2}+{n}_{+1}+{n}_{+2}}$
| p(X2≥k) | 0.05 | 0.01 |
| k | 3.841 | 6.635 |
(3)由于猜测员工的锻炼时间y与年龄x成线性相关,所以根据调查结果进行了线性回归分析,得到回归方程为y=-5x+b,如果员工的平均锻炼时间是110分钟,那么请判断下列说法的正误:
①b=285;
②由于回归方程的斜率是负的,说明年龄越大的员工,每周锻炼时间一定越短;
③由于回归直线方程的斜率是负的,说明两个变量的相关关系是负相关;
④能够算出回归方程,说明两个变旦之间确实是线性相关关系;
⑤回归直线是所有直线中穿过数据点最多的直线;
⑥两个变量是不是成线性相关关系还要看相关系数的大小.
分析 (1)补充2×2列联表,并计算出K2的值,与临界值比较后,可得是否“勒于锻炼者”与性别无关;
(2)由公司员工的年龄服从正态分布N(35,9),Φ(1)=0.8413,可得随机选取一名员工,他的年龄在32-38岁之间的概率为2×0.8413-1;
(3)根据回归方程及相关关系的相关概念逐一分析六个命题的真假,可得结论.
解答 解:(1)完整的2×2列联表如下表所示:
| “勤于锻炼者” | 非“勤于锻炼者” | 合计 | |
| 男 | 25 | 45 | 70 |
| 女 | 15 | 15 | 30 |
| 合计 | 40 | 60 | 100 |
故是否“勒于锻炼者”与性别无关;
(2)∵公司员工的年龄服从正态分布N(35,9),Φ(1)=0.8413,
∴从公司中随机选取一名员工,他的年龄在32-38岁之间的概率P=2×0.8413-1=0.6826
(3)由于猜测员工的锻炼时间y与年龄x成线性相关,所以根据调查结果进行了线性回归分析,得到回归方程为y=-5x+b,
如果员工的平均锻炼时间是110分钟,年龄的平均数为35,
故110=-5×35+b,
故b=285,即①正确;
由于回归方程的斜率是负的,说明年龄越大的员工,每周锻炼时间平均会越短,但不是一定变短,故②错误;
由于回归直线方程的斜率是负的,说明两个变量的相关关系是负相关,故③正确;
能够算出回归方程,但不能说明两个变旦之间确实是线性相关关系,故④错误;
回归直线可能不经过任何数据点,故⑤错误;
两个变量是不是成线性相关关系还要看相关系数的大小,故⑥正确.
故①③⑥正确;②④⑤错误;
点评 本题考查的知识是独立性检验,回归分析,正态分布,是统计和概率知识的综合应用,难度中档.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
17.在等比数列{an}中,a1=2,an+1=3an,则其前n项和为Sn的值为( )
| A. | 3n-1 | B. | 1-3n | C. | $\frac{1}{{{3^{n-1}}}}-1$ | D. | $1-\frac{1}{{{3^{n-1}}}}$ |