题目内容
【题目】为了了解学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,所得数据整理后,画出频率分布直方图(如图所示),图中从左到右各小长方形面积之比为![]() ,第二小组频数为
,第二小组频数为![]() .
.
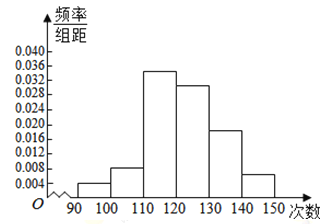
(1)学生跳绳次数的中位数落在哪个小组内?
(2)第二小组的频率是多少?样本容量是多少?
(3)若次数在![]() 以上(含
以上(含![]() 次)为良好,试估计该学校全体高一学生的良好率是多少?
次)为良好,试估计该学校全体高一学生的良好率是多少?
【答案】(1)中位数落在第四小组内;(2)0.08,150;(3)88%
【解析】
试题分析:(1)根据中位数落在的位置,刚好把频率分步直方图分成左右面积相等两部分,计算前三组与前四组的频率和即可得答案;(2)根据各个小矩形的面积之比,求出第二组的频率,再根据所给的频数,求出样本容量.(3)根据频率分步直方图求出次数在110以上的频数,用频数除以样本容量得到达标率,进而估计全体学生的达标率.
试题解析:(1)∵前三组的频率和为![]() ,
,
前四组的频率之和为![]() ,∴中位数落在第四小组内.
,∴中位数落在第四小组内.
(2)频率为:![]() ,又∵频率=
,又∵频率=![]() ,
,
∴样本容量=![]() .
.
(3)由图可估计所求良好率约为:![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】当今信息时代,众多高中生也配上了手机.某校为研究经常使用手机是否对学习成绩有影响,随机抽取高三年级50名理科生的一次数学周练成绩,用茎叶图表示如下图:

(1)根据茎叶图中的数据完成下面的![]() 列联表,并判断是否有95%的把握认为经常使用手机对学习成绩有影响?
列联表,并判断是否有95%的把握认为经常使用手机对学习成绩有影响?
及格( | 不及格 | 合计 | |
很少使用手机 | |||
经常使用手机 | |||
合计 |
(2)从50人中,选取一名很少使用手机的同学记为甲和一名经常使用手机的同学记为乙,解一道数列题,甲、乙独立解决此题的概率分别为![]() ,
, ![]() ,
, ![]() ,若
,若![]() ,则此二人适合结为学习上互帮互助的“师徒”,记
,则此二人适合结为学习上互帮互助的“师徒”,记![]() 为两人中解决此题的人数,若
为两人中解决此题的人数,若![]() ,问两人是否适合结为“师徒”?
,问两人是否适合结为“师徒”?
参考公式及数据:  ,其中
,其中![]() .
.
| <>0.10 | 0.05 | 0.025 |
| 2.706 | 3.841 | 5.024 |


