题目内容
【题目】已知![]() 是常数.
是常数.
(Ⅰ)求曲线![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(Ⅱ)设![]() ,讨论函数
,讨论函数![]() 的单调性.
的单调性.
【答案】(Ⅰ) ![]() ; (Ⅱ)
; (Ⅱ)![]() 在
在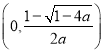 单调递增,在
单调递增,在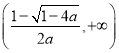 单调递减.
单调递减.
【解析】试题分析: (Ⅰ) 把x=1代入解析式求出切点坐标,对函数进行求导得到斜率,根据点斜式写出切线方程;(Ⅱ)把![]() 代入得到
代入得到![]() ,求出函数的导数,再进行配方判断导函数的正负,按照极值点是否在定义域内分四类进行讨论,得出函数的单调性.
,求出函数的导数,再进行配方判断导函数的正负,按照极值点是否在定义域内分四类进行讨论,得出函数的单调性.
试题解析:(Ⅰ) 因为![]() ,所以
,所以![]() ,故曲线
,故曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]()
(Ⅱ)因为![]()
所以![]()
①当![]() 时,
时, ![]() 在
在![]() 单调递增;
单调递增;
②当![]() 时,
时, ![]() 在
在![]() 单调递增,在
单调递增,在![]() 单调递减;
单调递减;
③当![]() 时,由
时,由![]() 得
得
![]()
所以, ![]() 在
在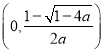 和
和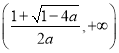 单调递增,在
单调递增,在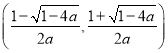 单调递减;
单调递减;
④当![]() 时,由
时,由![]() 得
得
![]() (
(![]() 舍去)
舍去)
所以, ![]() 在
在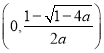 单调递增,在
单调递增,在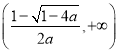 单调递减.
单调递减.
点睛:本题考查导数的几何意义和函数单调性的判断问题的综合应用,属于中档题目. 函数y=f(x)在x=x0处的导数的几何意义,就是曲线y=f(x)在点P(x0,y0)处的切线的斜率 ![]() ,过点P的切线方程为:
,过点P的切线方程为: ![]() ,求函数y=f(x)在点P(x0,y0)处的切线方程与求函数y=f(x)过点P(x0,y0)的切线方程意义不同,前者切线有且只有一条,且方程为y-y0=f′(x0)(x-x0),后者可能不只一条.
,求函数y=f(x)在点P(x0,y0)处的切线方程与求函数y=f(x)过点P(x0,y0)的切线方程意义不同,前者切线有且只有一条,且方程为y-y0=f′(x0)(x-x0),后者可能不只一条.

练习册系列答案
相关题目