题目内容
4.在△ABC中,角A,B,C的对边分别为a,b,c,若a2-b2-c2=-$\sqrt{3}$bc,则A等于( )| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
分析 利用余弦定理即可得出.
解答 解:∵a2-b2-c2=-$\sqrt{3}$bc,
∴b2+c2-a2=$\sqrt{3}$bc.
∴cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$=$\frac{\sqrt{3}}{2}$,
又A∈(0,π),
∴A=$\frac{π}{6}$.
故选:A.
点评 本题考查了余弦定理的应用,属于基础题.

练习册系列答案
相关题目
15.如果偶函数f(x)在[-7,-3]上是增函数且最小值是2,那么f(x)在[3,7]上是( )
| A. | 减函数且最小值是2 | B. | .减函数且最大值是2 | ||
| C. | 增函数且最小值是2 | D. | 增函数且最大值是2 |
19.甲、乙、丙、丁四人参加全运会射击项目选拔赛,四人的平均成绩和方差如表所示,从这四个人中选择一人参加全运会射击项目比赛,最佳人选是( )
| 甲 | 乙 | 丙 | 丁 | |
| 平均环数$\overline{x}$ | 7.5 | 8.7 | 8.7 | 8.4 |
| 方差s2 | 0.6 | 0.6 | 1.7 | 1.0 |
| A. | 甲 | B. | 乙 | C. | 丙 | D. | 丁 |
9.函数f(x)=-cosx•lg|x|的部分图象是( )
| A. | 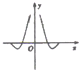 | B. | 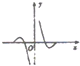 | C. | 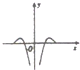 | D. | 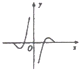 |
14.已知a、b分别为直线y=x+1的斜率与纵截距,复数z=$\frac{(a-i)(b+i)}{i}$在复平面上对应的点到原点的距离为( )
| A. | 1 | B. | 2 | C. | 4 | D. | $\sqrt{2}$ |