题目内容
4.若双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{m}$=1的焦距为6,则m的值为( )| A. | 32 | B. | 5 | C. | 8 | D. | -5 |
分析 利用双曲线的标准方程,求出a,b,c,利用双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{m}$=1的焦距是6,求出m的值.
解答 解:因为双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{m}$=1,所以a=2,b=$\sqrt{m}$,
又双曲线的焦距是6,所以6=2$\sqrt{4+m}$,
解得m=5.
故选:B.
点评 本题是基础题,考查双曲线的简单性质,双曲线的定义的应用,考查计算能力.

练习册系列答案
相关题目
12.“因为自然数是整数(大前提),而$\frac{1}{3}$是自然数(小前提),所以$\frac{1}{3}$是整数(结论)”,上面的推理是因为小前提(填“大前提”或“小前提”)错误导致结论错误.
19.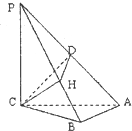 三棱锥P-ABC,PC⊥面ABC,△PAC是等腰三角形,PA=4,AB⊥BC,CH⊥PB,垂足为H,D是PA的中点,则△CDH的面积最大时,CB的长是( )
三棱锥P-ABC,PC⊥面ABC,△PAC是等腰三角形,PA=4,AB⊥BC,CH⊥PB,垂足为H,D是PA的中点,则△CDH的面积最大时,CB的长是( )
 三棱锥P-ABC,PC⊥面ABC,△PAC是等腰三角形,PA=4,AB⊥BC,CH⊥PB,垂足为H,D是PA的中点,则△CDH的面积最大时,CB的长是( )
三棱锥P-ABC,PC⊥面ABC,△PAC是等腰三角形,PA=4,AB⊥BC,CH⊥PB,垂足为H,D是PA的中点,则△CDH的面积最大时,CB的长是( )| A. | $\frac{\sqrt{5}}{3}$ | B. | $\frac{2\sqrt{5}}{3}$ | C. | $\frac{\sqrt{6}}{3}$ | D. | $\frac{2\sqrt{6}}{3}$ |
9.用一根长为12m的铝合金条做成一个“目”字形窗户的框架(不计损耗和边框粗细),则框架的最大面积为( )
| A. | 4m2 | B. | 6m2 | C. | 2.5m2 | D. | 4.5m2 |
13.在比赛中,如果运动员甲胜运动员乙的概率是$\frac{2}{3}$,那么在五次比赛中,运动员甲恰有三次获胜的概率是( )
| A. | $\frac{40}{243}$ | B. | $\frac{80}{243}$ | C. | $\frac{110}{243}$ | D. | $\frac{20}{243}$ |
14.已知等差数列{an}中,a1+a5=6,则a1+a2+a3+a4+a5=( )
| A. | 10$\sqrt{6}$ | B. | 5$\sqrt{6}$ | C. | 30 | D. | 15 |
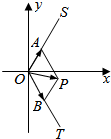 如图所示,A(m,$\sqrt{3}$m)和B(n,-$\sqrt{3}$n)两点分别在射线OS,OT(点S,T分别在第一,四象限)上移动,且$\overrightarrow{OA}$•$\overrightarrow{OB}$=-$\frac{1}{2}$,O为坐标原点,动点P满足$\overrightarrow{OP}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$.
如图所示,A(m,$\sqrt{3}$m)和B(n,-$\sqrt{3}$n)两点分别在射线OS,OT(点S,T分别在第一,四象限)上移动,且$\overrightarrow{OA}$•$\overrightarrow{OB}$=-$\frac{1}{2}$,O为坐标原点,动点P满足$\overrightarrow{OP}$=$\overrightarrow{OA}$+$\overrightarrow{OB}$.