题目内容
【题目】已知![]() ,
,![]() 是椭圆T.
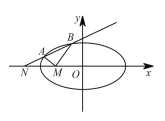
是椭圆T.![]() 上的两点,且A点位于第一象限.过A做x轴的垂线,垂足为点C,点D满足
上的两点,且A点位于第一象限.过A做x轴的垂线,垂足为点C,点D满足![]() ,延长
,延长![]() 交T于点
交T于点![]() .
.
(1)设直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() .
.
(i)求证:![]() ;
;
(ii)证明:![]() 是直角三角形;
是直角三角形;
(2)求![]() 的面积的最大值.
的面积的最大值.
【答案】(1)(i)见解析(ii)见解析(2)![]()
【解析】
(1)(i)求出点D的坐标,用![]() 、
、![]() 表示出
表示出![]() 、
、![]() 即可得证;(ii)利用
即可得证;(ii)利用![]() ,
,![]() 都在T上可将两点坐标代入椭圆方程,两式相减并通过变形证明
都在T上可将两点坐标代入椭圆方程,两式相减并通过变形证明![]() ,由(i)可推出
,由(i)可推出![]() ,则
,则![]() ,得证;(2)直线AE的方程代入椭圆方程整理得关于x的一元二次方程,利用韦达定理求出
,得证;(2)直线AE的方程代入椭圆方程整理得关于x的一元二次方程,利用韦达定理求出![]() ,由
,由![]() 求出面积的表达式,利用换元法及对勾函数的单调性即可求得面积的最大值.
求出面积的表达式,利用换元法及对勾函数的单调性即可求得面积的最大值.
(1)(i)由题意可得![]() ,所以
,所以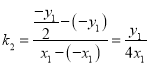 ,
,
又![]() ,因此
,因此![]() .
.
(ii)因为![]() ,
,![]() 都在T上,
都在T上,
所以![]() ,
,![]() ,从而
,从而![]() ,
,
即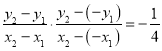 .
.
又![]() ,
,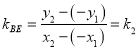 ,所以
,所以![]() ,
,
由(i)![]() ,则
,则![]() ,即
,即![]() .
.
故![]() 是直角三角形.
是直角三角形.
(2)由(1)得,![]() :
:![]() ,
,
将直线![]() 代入椭圆T,并整理可得
代入椭圆T,并整理可得![]() ,
,
所以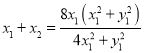 .
.
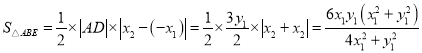 ,
,
因为![]() ,所以
,所以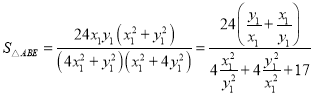 .
.
令![]() ,则
,则![]() ,等号当且仅当
,等号当且仅当![]() 时成立.
时成立.
从而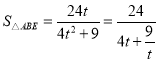 ,
,
因为![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() 时,
时,![]() 取得最小值
取得最小值![]() ,
,
故![]() 时,
时,![]() 取得最大值
取得最大值![]() .
.

练习册系列答案
相关题目