Question

【题目】已知椭圆的右焦点为，过点且与轴垂直的直线被椭圆截得的线段长为，且与短轴两端点的连线相互垂直.

（1）求椭圆的方程；

（2）若圆上存在两点，，椭圆上存在两个点满足：三点共线，三点共线，且，求四边形面积的取值范围.

Answer 1

【答案】（1）；（2）

【解析】

（1）又题意知，，及即可求得，从而得椭圆方程.

（2）分三种情况：直线斜率不存在时，的斜率为0时，的斜率存在且不为0时，设出直线方程，联立方程组，用韦达定理和弦长公式以及四边形的面积公式计算即可.

（1）由焦点与短轴两端点的连线相互垂直及椭圆的对称性可知，，

∵过点且与轴垂直的直线被椭圆截得的线段长为.

又，解得.

∴椭圆的方程为

（2）由（1）可知圆的方程为，

（i）当直线的斜率不存在时，直线的斜率为0，

此时

（ii）当直线的斜率为零时，.

（iii）当直线的斜率存在且不等于零时，设直线的方程为，

联立，得，

设的横坐标分别为，则.

所以，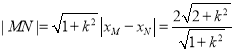

（注：的长度也可以用点到直线的距离和勾股定理计算.）

由可得直线的方程为，联立椭圆的方程消去，

得

设的横坐标为，则.

.

综上，由（i）（ii）（ⅲ）得的取值范围是.