题目内容
9.解下列不等式:|x+3|+|2x-3|≥3.分析 把要解的不等式等价转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.
解答 解:|x+3|+|2x-3|≥3,等价于 $\left\{\begin{array}{l}{x<-3}\\{-x-3+3-2x≥3}\end{array}\right.$ ①,或$\left\{\begin{array}{l}{-3≤x<\frac{3}{2}}\\{x+3+3-2x≥3}\end{array}\right.$ ②,或$\left\{\begin{array}{l}{x≥\frac{3}{2}}\\{x+3+2x-3≥3}\end{array}\right.$③.
解①求得x<-3,解②求得-3≤x<$\frac{3}{2}$,解③求得x≥$\frac{3}{2}$,
综合可得原不等式的解集为{x|x∈R}=R.
点评 本题主要考查绝对值不等式的解法,体现了转化、分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目
8.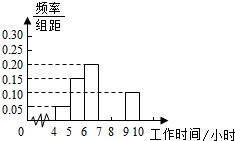 某高新区一工厂为了了解工人的工作时间(单位:小时),从该工厂抽取20名工人的工作时间作为样本进行调查,调查的数据分组整理后如表所示,并作出样本的部分频率分布直方图如图.
某高新区一工厂为了了解工人的工作时间(单位:小时),从该工厂抽取20名工人的工作时间作为样本进行调查,调查的数据分组整理后如表所示,并作出样本的部分频率分布直方图如图.
(1)求表中a,b,x的值,并补齐频率分布直方图;
(2)现从工作时间在[4,5]和[6,7)内的工人中随机抽取2名,求抽到的2名工人的工作时间都在[6,7)内的概率.
 某高新区一工厂为了了解工人的工作时间(单位:小时),从该工厂抽取20名工人的工作时间作为样本进行调查,调查的数据分组整理后如表所示,并作出样本的部分频率分布直方图如图.
某高新区一工厂为了了解工人的工作时间(单位:小时),从该工厂抽取20名工人的工作时间作为样本进行调查,调查的数据分组整理后如表所示,并作出样本的部分频率分布直方图如图.| 工作时间(小时) | [4,5) | [5,6) | [6,7) | [7,8) | [8,9) | [9,10) |
| 频数 | 1 | 3 | 4 | a | b | 2 |
| 频率 | 0.05 | 0.15 | 0.20 | 0.30 | x | 0.10 |
(2)现从工作时间在[4,5]和[6,7)内的工人中随机抽取2名,求抽到的2名工人的工作时间都在[6,7)内的概率.