题目内容
8.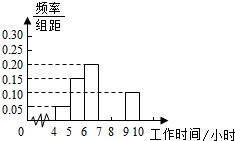 某高新区一工厂为了了解工人的工作时间(单位:小时),从该工厂抽取20名工人的工作时间作为样本进行调查,调查的数据分组整理后如表所示,并作出样本的部分频率分布直方图如图.
某高新区一工厂为了了解工人的工作时间(单位:小时),从该工厂抽取20名工人的工作时间作为样本进行调查,调查的数据分组整理后如表所示,并作出样本的部分频率分布直方图如图.| 工作时间(小时) | [4,5) | [5,6) | [6,7) | [7,8) | [8,9) | [9,10) |
| 频数 | 1 | 3 | 4 | a | b | 2 |
| 频率 | 0.05 | 0.15 | 0.20 | 0.30 | x | 0.10 |
(2)现从工作时间在[4,5]和[6,7)内的工人中随机抽取2名,求抽到的2名工人的工作时间都在[6,7)内的概率.
分析 (1)根据题意,求出a、b与x的值,补齐频率分布直方图即可;
(2)用列举法计算基本事件数,求出对应的概率即可
解答 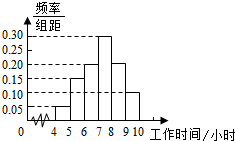 解:(1)根据题意,a=20×0.30=6,
解:(1)根据题意,a=20×0.30=6,
b=20-(1+3+4+6+2)=4,
x=$\frac{4}{20}$=0.20;
∵[7,8)对应的小矩形的高为0.30,
[8,9)对应的小矩形的高为0.20,
∴补齐频率分布直方图如图所示;
(2)工作时间在[4,5]的人数是1,记为A;
工作时间在[6,7)内的人数是4,分别记为b、c、d、e;
现从这5人中随机抽取2名,基本事件是
Ab、Ac、Ad、Ae、bc、bd、be、cd、ce、de,共种10;
其中抽到的2名工人的工作时间都在[6,7)内的基本事件是
bc、bd、be、cd、ce、de,共6种;
所求的概率为P=$\frac{6}{10}$=$\frac{3}{5}$.
点评 本题考查了频率分布直方图的应用问题,也考查了利用列举法求古典概型的概率问题,是基础题目.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
20.钝角三角形ABC的面积为3$\sqrt{3}$,BC=3,AC=4,则AB=( )
| A. | $\sqrt{13}$ | B. | $\sqrt{37}$ | C. | 6 | D. | 7 |