题目内容
5.下面有三个命题:(1)函数y=sin($\frac{2}{3}$x+$\frac{π}{2}$)是偶函数;
(2)函数f (x)=|2cos2x-1|的最小正周期是π;
(3)函数f (x)=sin(x+$\frac{π}{4}$)在[-$\frac{π}{2}$,$\frac{π}{2}$]上是增函数;
其中正确命题的序号是(1).
分析 利用诱导公式化简(1)后判断;利用倍角公式化简(2),再由y=|cos2x|的周期为y=cos2x周期的一半判断(2);求出函数f (x)=sin(x+$\frac{π}{4}$)的增区间判断(3).
解答 解:(1)函数y=sin($\frac{2}{3}$x+$\frac{π}{2}$)=cos$\frac{2}{3}x$是偶函数,命题(1)正确;
(2)函数f (x)=|2cos2x-1|=|cos2x|,最小正周期是$\frac{π}{2}$,命题(2)错误;
(3)由$-\frac{π}{2}+2kπ≤x+\frac{π}{4}≤\frac{π}{2}+2kπ$,得$-\frac{3π}{4}+2kπ≤x≤\frac{π}{4}+2kπ,k∈Z$,
取k=0,得$-\frac{3π}{4}≤x≤\frac{π}{4}$,∴函数f (x)=sin(x+$\frac{π}{4}$)在[-$\frac{π}{2}$,$\frac{π}{2}$]上不是增函数.
∴正确命题的序号是(1).
故答案为:(1).
点评 本题考查命题的真假判断与应用,考查了三角函数的图象和性质,关键是对三角函数性质的记忆,是基础题.

练习册系列答案
相关题目
17.小明同学每天下午4:00到5:00之间放学到家学习,小刚同学每天下午4:30到5:30之间到达小明家给他辅导功课,则小刚到小明家时就能见到小明的概率是( )
| A. | 1 | B. | 0.875 | C. | 0.65 | D. | 0.5 |
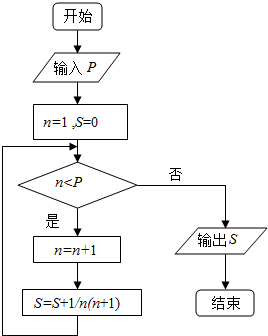 执行如图的程序框图,若p=7,则输出的s=$\frac{3}{8}$.
执行如图的程序框图,若p=7,则输出的s=$\frac{3}{8}$.