题目内容
16.已知函数f(x)=loga[(a-1)x-1].(1)求函数f(x)的定义域;
(2)若对任意x∈[2,+∞)恒有f(x)>0,试确定a的取值范围.
分析 (1)由真数大于零可求出答案;
(2)利用函数的单调性求出f(x)的最小值,只需让f(x)的最小值大于0即可.
解答 解:(1)由f(x)=loga[(a-1)x-1]有意义得:
(a-1)x-1>0,且a>0,a≠1
当a>1时,x>$\frac{1}{a-1}$;
当0<a<1时,x<$\frac{1}{a-1}$.
∴当a>1时,f(x)的定义域为($\frac{1}{a-1}$,+∞);
当0<a<1时,f(x)的定义域为(-∞,$\frac{1}{a-1}$).
(2)令g(x)=(a-1)x-1,
则当a>1时,g(x)=(a-1)x-1在[2,+∞)上是增函数,
∴f(x)=loga[(a-1)x-1]在[2,+∞)上是增函数.
当0<a<1时,g(x)=(a-1)x-1在[2,+∞)上是减函数,
∴f(x)=loga[(a-1)x-1]在[2,+∞)上是增函数.
综上所述,f(x)=loga[(a-1)x-1]在[2,+∞)上是增函数.
∴fmin(x)=f(2)=loga(2a-3).
∵对任意x∈[2,+∞)恒有f(x)>0,
∴fmin(x)>0,
即loga(2a-3)>0.
①当a>1时,2a-3>1,解得a>2.
②0<a<1时,0<2a-3<1解得$\frac{3}{2}$<a<2(舍).
a的取值范围是(2,+∞).
点评 本题主要考查了对数函数的定义域、复合函数的单调性及分类讨论思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.集合{x|x≥2}表示成区间是( )
| A. | (2,+∞) | B. | [2,+∞) | C. | (-∞,2) | D. | (-∞,2] |
8.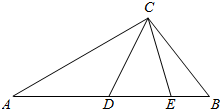 如图△ABC中,C=$\frac{π}{2}$,AC=$\sqrt{3}$,BC=1,D,E为线段AB的点,∠ACD=$\frac{π}{4}$,∠DCE=$\frac{π}{6}$,则△DCE的面积为( )
如图△ABC中,C=$\frac{π}{2}$,AC=$\sqrt{3}$,BC=1,D,E为线段AB的点,∠ACD=$\frac{π}{4}$,∠DCE=$\frac{π}{6}$,则△DCE的面积为( )
 如图△ABC中,C=$\frac{π}{2}$,AC=$\sqrt{3}$,BC=1,D,E为线段AB的点,∠ACD=$\frac{π}{4}$,∠DCE=$\frac{π}{6}$,则△DCE的面积为( )
如图△ABC中,C=$\frac{π}{2}$,AC=$\sqrt{3}$,BC=1,D,E为线段AB的点,∠ACD=$\frac{π}{4}$,∠DCE=$\frac{π}{6}$,则△DCE的面积为( )| A. | $\frac{6-3\sqrt{3}}{4}$ | B. | $\frac{9-3\sqrt{3}}{8}$ | C. | $\frac{1}{4}$ | D. | $\frac{\sqrt{3}}{8}$ |