题目内容
10.若sinθ=$\frac{m-3}{m+5}$,cosθ=$\frac{4-2m}{m+5}$,θ∈($\frac{π}{2}$,π),则m的取值范围是{8}.分析 通过平方关系得到关于m的表达式,求出m的值,结合三角函数的性质,判断m的值即可.
解答 解:∵sin2θ+cos2θ=1
∴$\frac{(m-3)^{2}}{(m+5)^{2}}$+$\frac{(4-2m)^{2}}{(m+5)^{2}}$=1,
∴(m-3)2+(4-2m)2=(m+5)2
即m2-6m+9+16-16m+4m2=m2+10m+25
即25-22m+4m2=10m+25
即-32m+4m2=0
即m=0,或m=8
因为$\frac{π}{2}$<θ<π,当m=0时,sinθ=-
| 3 |
| 5 |
所以m=8
故答案为:{8}
点评 本题考查同角三角函数的基本关系式的应用,考查计算能力,象限角三角函数值的符号,是基础题

练习册系列答案
相关题目
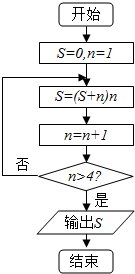
15.如图是某算法的程序框图,则输出的S=( )

| A. | 6 | B. | 27 | C. | 124 | D. | 604 |
 为了解某省去年高三考生英语听力成绩,现从某校高三年级随机抽取50名考生的成绩,发现全部介于[6,30]之间,将成绩按如下方式分成6组:第1组[6,10),第2组[10,14),…,第6组[26,30],如图是按上述分组方法得到的频率分布直方图.
为了解某省去年高三考生英语听力成绩,现从某校高三年级随机抽取50名考生的成绩,发现全部介于[6,30]之间,将成绩按如下方式分成6组:第1组[6,10),第2组[10,14),…,第6组[26,30],如图是按上述分组方法得到的频率分布直方图. 在某中学举行的环保知识竞赛中,随机抽取x名参赛同学的成绩(得分的整数)进行整理后分成五组,绘制出如图所示的频率分布直方图,已知图中从左到右的第一、第三、第四、第五小组的频率分别为0.30,0.15,0.10,0.05,第二小组的频数为40.
在某中学举行的环保知识竞赛中,随机抽取x名参赛同学的成绩(得分的整数)进行整理后分成五组,绘制出如图所示的频率分布直方图,已知图中从左到右的第一、第三、第四、第五小组的频率分别为0.30,0.15,0.10,0.05,第二小组的频数为40. 某楼盘开展套餐促销优惠活动,优惠方案如下:选择套餐一的客户可获得优惠2万元,选择套餐二的客户可获得优惠5万元,选择套餐三的客户可获得优惠3万元.根据以往的统计结果绘出参与活动的统计图如图所示,现将频率视为概率.
某楼盘开展套餐促销优惠活动,优惠方案如下:选择套餐一的客户可获得优惠2万元,选择套餐二的客户可获得优惠5万元,选择套餐三的客户可获得优惠3万元.根据以往的统计结果绘出参与活动的统计图如图所示,现将频率视为概率.