题目内容
13．某学校有教师132人，职工33人，学生1485人．为了解食堂情况，拟采用分层抽样的方法从以上人员中抽取50人进行抽查，则在学生中应抽取45 人．分析 本题是一个分层抽样方法，根据总体数和要抽取的样本数，得到每个个体被抽到的概率，利用这个概率乘以学生人数，得到学生要抽取的人数．
解答 解：由题意知本题是一个分层抽样方法，
∵学校有教师132人，职工33人，学生1485人，采用分层抽样的方法从以上人员中抽取50人进行抽查，
∴每个个体被抽到的概率是$\frac{50}{132+33+1485}$=$\frac{1}{33}$
∵学生1485人，∴在学生中应抽取1485×$\frac{1}{33}$=45
故答案为：45
点评 本题考查分层抽样方法，本题解题的关键是在抽样过程中每个个体被抽到的概率相等，本题是一个基础题．
练习册系列答案
相关题目
3．在△ABC所在平面上有三点P、Q、R，满足$\overrightarrow{PC}$=2$\overrightarrow{AP}$，$\overrightarrow{QA}$=2$\overrightarrow{BQ}$，$\overrightarrow{RB}$=2$\overrightarrow{CR}$，则△PQR的面积与△ABC的面积之比为（ ）
| A． | 1：5 | B． | 1：4 | C． | 1：3 | D． | 1：2 |
4．集合{x|x≥2}表示成区间是（ ）
| A． | （2，+∞） | B． | [2，+∞） | C． | （-∞，2） | D． | （-∞，2] |
8．
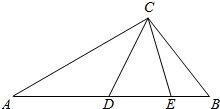如图△ABC中，C=$\frac{π}{2}$，AC=$\sqrt{3}$，BC=1，D，E为线段AB的点，∠ACD=$\frac{π}{4}$，∠DCE=$\frac{π}{6}$，则△DCE的面积为（ ）
如图△ABC中，C=$\frac{π}{2}$，AC=$\sqrt{3}$，BC=1，D，E为线段AB的点，∠ACD=$\frac{π}{4}$，∠DCE=$\frac{π}{6}$，则△DCE的面积为（ ）| A． | $\frac{6-3\sqrt{3}}{4}$ | B． | $\frac{9-3\sqrt{3}}{8}$ | C． | $\frac{1}{4}$ | D． | $\frac{\sqrt{3}}{8}$ |
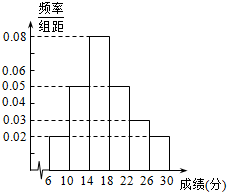为了解某省去年高三考生英语听力成绩，现从某校高三年级随机抽取50名考生的成绩，发现全部介于[6，30]之间，将成绩按如下方式分成6组：第1组[6，10），第2组[10，14），…，第6组[26，30]，如图是按上述分组方法得到的频率分布直方图．
在某中学举行的环保知识竞赛中，随机抽取x名参赛同学的成绩（得分的整数）进行整理后分成五组，绘制出如图所示的频率分布直方图，已知图中从左到右的第一、第三、第四、第五小组的频率分别为0.30，0.15，0.10，0.05，第二小组的频数为40．