题目内容
【题目】已知函数![]() ,
, ![]() .
.
(1)当![]() 时,求不等式
时,求不等式![]() 的解集;
的解集;
(2)若不等式![]() 的解集包含
的解集包含![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1){x|-3≤x≤1}(2)[1,3]
【解析】试题分析:
(1)由题意得不等式即为|x+1|-|x-1|≥x2+3x-2,根据分类讨论的方法将不等式转化为三个不等式组求解.(2)令F(x)=g(x)-f(x)=x2+(a-2)x-2,将不等式![]() 的解集包含
的解集包含![]() 转化为
转化为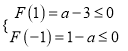 求解即可得结论.
求解即可得结论.
试题解析:
(1)不等式|x+1|-|x-1|≥x2+3x-2等价于
![]() 或
或![]() 或
或![]()
解得 ,或-1≤x≤1,或-3≤x<-1.
所以不等式f(x)≥g(x)的解集是{x|-3≤x≤1}.
(2)x∈[-1,1],令F(x)=g(x)-f(x)=x2+(a-2)x-2
不等式f(x)≥g(x)的解集包含[-1,1]等价于
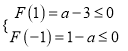
解得1≤a≤3,
所以a的取值范围为[1,3].

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目