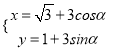题目内容
【题目】已知抛物线![]() :
: ![]() 的焦点,过点
的焦点,过点![]() 作两条互相垂直的直线
作两条互相垂直的直线![]() ,直线
,直线![]() 交
交![]() 于不同的两点
于不同的两点![]() ,直线
,直线![]() 交
交![]() 于不同的两点
于不同的两点![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() .
.
(1)求![]() 的取值范围;
的取值范围;
(2)设线段![]() 的中点分别为点
的中点分别为点![]() ,证明:直线
,证明:直线![]() 过定点
过定点![]() .
.
【答案】(1) {k|k<-2或0<k<![]() } (2)见解析
} (2)见解析
【解析】试题分析:
(1)写出直线![]() 的方程
的方程![]() ,与抛物线方程联立方程组,利用判别式求出
,与抛物线方程联立方程组,利用判别式求出![]() 的一个范围,另外直线
的一个范围,另外直线![]() 的方程为
的方程为![]() 与抛物线方程联立同样又得出
与抛物线方程联立同样又得出![]() 的一个范围,两者求交集即得;
的一个范围,两者求交集即得;
(2)设![]() ,利用韦达定理可得
,利用韦达定理可得![]() 即
即![]() 点坐标,用
点坐标,用![]() 代替
代替![]() 可得
可得![]() 点坐标,计算出
点坐标,计算出![]() ,得证结论.
,得证结论.
试题解析:
(1)由题设可知k≠0,所以直线m的方程为y=kx+2,与y2=4x联立,
整理得ky2-4y+8=0, ①
由Δ1=16-32k>0,解得k<![]() .
.
直线n的方程为y=-![]() x+2,与y2=4x联立,
x+2,与y2=4x联立,
整理得y2+4ky-8k=0,
由Δ2=16k2+32k>0,解得k>0或k<-2.
所以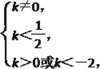 故k的取值范围为{k|k<-2或0<k<
故k的取值范围为{k|k<-2或0<k<![]() }.
}.
(2)设A(x1,y1),B(x2,y2),M(x0,y0).
由①得,y1+y2=![]() ,则y0=
,则y0=![]() ,x0=
,x0=![]() -
-![]() ,则M(
,则M(![]() -
-![]() ,
,![]() ).
).
同理可得N(2k2+2k,-2k).
直线MQ的斜率kMQ=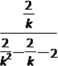 =
=![]() ,
,
直线NQ的斜率kNQ=![]() =
=![]() =kMQ,
=kMQ,
所以直线MN过定点Q(2,0).

【题目】汽车是碳排放量比较大的交通工具,某地规定,从2017年开始,将对二氧化碳排放量超过130 g/km的轻型汽车进行惩罚性征税,检测单位对甲、乙两品牌轻型汽车各抽取5辆进行二氧化碳排放量检测,记录如下(单位:g/km):
甲 | 80 | 110 | 120 | 140 | 150 |
乙 | 100 | 120 | x | 100 | 160 |
经测算得乙品牌轻型汽车二氧化碳排放量的平均值为![]() =120 g/km.
=120 g/km.
(1)求表中x的值,并比较甲、乙两品牌轻型汽车二氧化碳排放量的稳定性;
(2)从被检测的5辆甲品牌轻型汽车中任取2辆,则至少有一辆二氧化碳排放量超过130 g/km的概率是多少?